



Функции имеющие не более конечного числа разрывов 1-го рода на отрезке [a,b]. (их называют кусочно-непрерывными)
3. Функции монотонные на отрезке [a,b] (у функции этого класса число разрывов может быть бесконечным).
1) Если ![]() непрерывна на
непрерывна на ![]() , то она интегрируема (ограничена).
, то она интегрируема (ограничена).
2) Если ограниченная функция ![]() на
на
![]() имеет лишь конечное число точек разрыва,
то она интегрируема на
имеет лишь конечное число точек разрыва,
то она интегрируема на ![]() .
.
3) Монотонная ограниченная функция ![]() всегда интегрируема.
всегда интегрируема.
Th1. Пусть надо вычислить н.и. ![]() .
Если функция
.
Если функция ![]() дифференцируема на
дифференцируема на ![]() и
и ![]() интеграл
интеграл
![]() на промежутке
на промежутке ![]() ,
тогда (1)
,
тогда (1) ![]() на
на ![]() .
.
Формулу (1) часто записывают в виде:
![]() (1)’
(1)’
После вычисления интеграла
справа, вместо t подставим ![]() .Формулы (1) и (1)’
получаются, если бы мы ввели вместо
.Формулы (1) и (1)’
получаются, если бы мы ввели вместо ![]() переменную
t,
переменную
t, ![]() .
.![]()
Пример: ![]()
Th2.
Пусть надо вычислить интеграл ![]() . Если некоторая
функция
. Если некоторая
функция ![]() дифференцируема на
дифференцируема на ![]() и
и ![]() на
на ![]() , то (2)
, то (2) ![]()
В формуле (2) мы формально вводим новую функцию ![]() .
.
![]()
Всякая рациональная дробь
представима в виде ![]() .
.
Если m≥n – дробь
неправильная, выделяем целую часть : ![]() .
.
Всякую правильную рац.
дробь, знаменатель которой разложен на множители ![]() , (множители
, (множители
![]() должны
быть неразложимыми т.е.
должны
быть неразложимыми т.е. ![]() ), можно
представить в виде суммы простейших дробей:
), можно
представить в виде суммы простейших дробей: ![]() .
.
Далее:
В правой части приводим к
общему знаменателю ![]() . Получаем
. Получаем ![]() , где
, где ![]() -многочлен
с неопределёнными коэф-ми. Из этого получаем
-многочлен
с неопределёнными коэф-ми. Из этого получаем ![]() .Приравнивая
коэф-ты при одинаковых степенях, получаем систему лин. уравнений, из которой
получаем искомые коэф-ты.
.Приравнивая
коэф-ты при одинаковых степенях, получаем систему лин. уравнений, из которой
получаем искомые коэф-ты.
1) ![]() .
.
2) ![]()
3) ![]() ,
,
J2: ![]()
4)![]()
□ 1. Неопределенный интеграл. Свойства неопределенного интеграла
□ 2. Классы интегрируемых функций
□ 3. Замена переменной в неопределенном интеграле.
□ 4 . Интегрирование рациональных дробей
□ 5. Интегрирование простейших дробей 1, 2, 3 типов
1. Интеграл
вида ![]() ,
подстановкой
,
подстановкой ![]() сводится
к интегралу от рациональной функции относительно t.
сводится
к интегралу от рациональной функции относительно t.
2. ![]() в
этом случае заменой
в
этом случае заменой ![]() , где s-наименьшее
общее кратное чисел m..n.
, где s-наименьшее
общее кратное чисел m..n.
3. ![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
4. ![]() выделяем полный квадрат и подстановку
выделяем полный квадрат и подстановку ![]()
5. ![]() ;
; ![]() ;
; ![]() : выделяем полный квадрат
: выделяем полный квадрат ![]() , и
подстановку
, и
подстановку ![]() .
.
1) Универсальная тригон-я
подстановка.![]() :
:
![]()
2) если ф.![]() :
:
а) нечётна отн sinx
(![]() ), то t=cosx;
), то t=cosx;
б) нечётна отн cosx
(![]() ), то t=sinx;
), то t=sinx;
в) чётна отн cosx
и sinx (![]() ), то t=tgx;
), то t=tgx;
3)![]()
а) t=sinx, n- целое “+” нечётное число б)t=cosx, m-целое “+” нечётное число в)t=tgx, m+n- чётное “-“ целое число г)формулы понижения порядка если m и n – целые неотрицат. чётные числа.
![]()
![]()
![]() .
.
4) тригонометрич преобразования
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
![]()
Выражается если:
1) p-целое число ![]() , где k –наименьшее
общее кратное дробей m и n.
, где k –наименьшее
общее кратное дробей m и n.
2) ![]() – целое
число
– целое
число ![]() , где s-знаменатель
дроби p.
, где s-знаменатель
дроби p.
3) ![]() – целое
число
– целое
число ![]() , где s-знаменатель
дроби p.
, где s-знаменатель
дроби p.
Во всех остальных случаях такие интегралы «не берутся».
Всякое подынтегральное
выражение можно представить в виде ![]() , где
, где ![]() -ф.
переем-й интегрирования.
-ф.
переем-й интегрирования.
Интегрированием по частям
наз-ся сведение ![]() к
к ![]() .
.
Th. Пусть ![]() дифференцируемы
на <a,b> и
дифференцируемы
на <a,b> и ![]() , тогда
сущ-ет
, тогда
сущ-ет ![]() ;
;![]() .
.
Пример: ![]()
Пусть функция определена на отрезке [a,b].
1) Точками a=x0…xn=b разобьём торезок на n отрезков.
2) В каждом отрезке выберем
произвольную точку ![]() , и
вычислим значение ф. в ней
, и
вычислим значение ф. в ней ![]() .
.
3) умн-м ![]() . на длину
отрезка
. на длину
отрезка ![]() :
:
![]() .
.
4) Cоcтавим сумму из всех произведений (интегральная сумма):
![]() 5) Обозначим через λ длину
наибольшего частичного отрезка
5) Обозначим через λ длину
наибольшего частичного отрезка ![]() данного
разбиения.
данного
разбиения.
Определенным интегралом от
функции ![]() на отрезке
на отрезке ![]() называется
конечный предел I интегральной суммы
называется
конечный предел I интегральной суммы ![]() , если
такой предел существует:
, если
такой предел существует:![]() .
.
□ 6. Интегрирование иррациональных выражений
□ 7. Интегрирование тригонометрических функций
□ 8. Интегрирование дифференциального бинома
□ 9. Интегрирование по частям
□ 10. Интегральная сумма. Понятие определенного интеграла
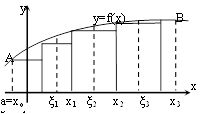
Найдем площадь:
1) разобьем отрезок [a,b] на n частей точками a = xo < x1 < x2 <…< xi-1 < xi <..< xn = b.
2) через точки деления проведем прямые параллельные оси Оу. В каждом частичном отрезке
[Xo , X1] , [ X1,X2 ] , … [ Xi-1, Xi ] … [ Xn-1, Xn ] выберем произвольные точки
Найдем значения функции в этих точках ƒ(ζ1), ƒ(ζ2), ƒ(ζi), ƒ(ζn), и найдем сумму площадей прямоугольников с основанием Δхi = хi – хi-1, i=1,n .
Сумма площадей прямоугольников равна:
![]() , за
площадь криволинейной трапеции принимается предел, к которому стремится эта
сумма:
, за
площадь криволинейной трапеции принимается предел, к которому стремится эта
сумма:
![]() .
.
Т.е.
Геометрический смысл определенного интеграла: Определенный интеграл от не отрицательной ф-ии равен площади соответствующей криволинейной трапеции.
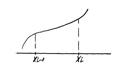
Обозначим через ![]() и
и ![]() точные
нижнюю и верхнюю границы для функции
точные
нижнюю и верхнюю границы для функции ![]() в
в ![]() -том
частичном промежутке
-том
частичном промежутке ![]() .
.
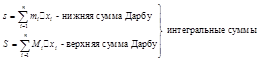 Из
определений нижней и верхней границ имеем
Из
определений нижней и верхней границ имеем ![]() ,
поэтому умножив все части неравенства на
,
поэтому умножив все части неравенства на ![]() и
просуммировав их, получим
и
просуммировав их, получим ![]() .
.
При заданном
разбиении промежутка суммы Дарбу ![]() и
и ![]() служат точными нижней и верхней
границами для интегральных сумм.
служат точными нижней и верхней
границами для интегральных сумм.
Теорема.
Для того, чтобы определенный
интеграл существовал, необходимо и достаточно, чтобы ![]() .
.
1) ![]()
2) ![]()
3) ![]()
4) Если [a,b] точкой c делится на 2 отрезок [a,c] и [c,b], то
![]() =
= ![]() +
+ ![]() .
.
5) Если на отрезке [a,b] ƒ1(х)≥
ƒ2(х), то ![]() .
.
6) Если функция непрерывна
на [a,b], то найдется точка ![]() ,такая что
:
,такая что
:
![]() =c (b – a);
=c (b – a);
7) ![]() ≤
≤ ![]()
8) Если функция y = ƒ(х) непрерывна на отрезке [a,b], то
m(b-a) ≤ ![]() ≤ M(b-a); m-наим-ее
значение ф. M-наиб. на отрезке на [a,b].
≤ M(b-a); m-наим-ее
значение ф. M-наиб. на отрезке на [a,b].
Если функция y = ƒ(х) непрерывна на отрезке [a,b] (m-наим-ее значение ф. M-наиб. на отрезке на [a,b]), то
m(b-a) ≤ ![]() ≤ M(b-a);.
≤ M(b-a);.
![]() .
.
![]() .
.
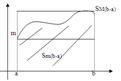
Геом смысл: ![]()
Пусть ![]() – непрерывная функция на отрезке
– непрерывная функция на отрезке ![]() , функция
, функция ![]() непрерывна
и дифференцируема на
непрерывна
и дифференцируема на ![]() ,
,![]() и
и ![]() .Тогда верна формула
.Тогда верна формула ![]() .
.
Доказательство: По формуле Ньютона-Лейбница
![]() где
где![]() – первообразная для
– первообразная для ![]() на
на![]() . Т.к.
. Т.к.
![]() . То
. То ![]() является
первообразной для функции
является
первообразной для функции![]() . Поэтому, согласно
формуле Ньютона-Лейбница получаем:
. Поэтому, согласно
формуле Ньютона-Лейбница получаем:
![]() .
.![]()
□ 11. Определенный интеграл. Механический и геометрический смысл
□ 12. Суммы Дарбу
□ 13. Свойства определенного интеграла
□ 14. Оценка интеграла
□ 15. Замена переменной в определенном интеграле
Определенный интеграл можно выразить многообразными геометрическими и физическими величинами. При этом применяется следующая единообразная схема:
1) искомая величина ![]() ставится
в соответствие с промежутком
ставится
в соответствие с промежутком ![]() некоторого изменения
аргумента;
некоторого изменения
аргумента;
2) промежуток ![]() разбивается на части
разбивается на части ![]() (в дальнейшем будем считать
(в дальнейшем будем считать ![]() , а длины промежутков
, а длины промежутков ![]() ). Пусть искомая величина
). Пусть искомая величина ![]() распадается на части
распадается на части ![]() , причем
, причем ![]() ;
;
3) в качестве типичного представителя частей ![]() берется одна из них
берется одна из них ![]() . Она выражается (исходя их условия
задачи) приближенной формулой следующего вида:
. Она выражается (исходя их условия
задачи) приближенной формулой следующего вида: ![]() ;
;
4) с увеличением числа ![]() погрешность
погрешность
![]() должна стремиться к нулю, поэтому
искомая величина
должна стремиться к нулю, поэтому
искомая величина ![]() есть предел этой суммы, т.е.
есть предел этой суммы, т.е. ![]() .
.
Пусть на отрезке [a;b] ф-я y = f(x) неотрицательна.
Тогда Sкрив. трап., огран. этой кривой, осью
ОХ и прямыми х=а, х=b , S = ∫ f(x)dx
Если f(x)≤0, то -S = ∫ f(x)dx , S = - ∫ f(x)dx
Если ф-я - конечное число
раз меняет знак на отр. [a;b], то инт-л по всему отр. разбиваем на сумму инт-лов
по частичн. отрезкам. S=∫│f(x)│dx. ![]()
Если же требуется найти S фигуры, ограничен. кривыми y=f1(x) и y=f2(x), причем f1(x) £ f2(x) на отрезке [a;b], то S=∫[ f2(x) - f1(x) ]dx
ПАРАМЕТРИЧЕСКИ:
![]() ,
,![]()
![]() .
.
ДАЛЕЕà
Пусть ![]() неопределенная функция, имеющая
неопределенную производную. Ее графиком является линия. Длиной дуги кривой
линии назовем предел, к которому стремится длина вписанной в нее ломаной при
неограниченном увеличении числа ее сторон и при стремлении наибольшей из этих
сторон к нулю.
неопределенная функция, имеющая
неопределенную производную. Ее графиком является линия. Длиной дуги кривой
линии назовем предел, к которому стремится длина вписанной в нее ломаной при
неограниченном увеличении числа ее сторон и при стремлении наибольшей из этих
сторон к нулю.
Итак,
пусть линия ![]() задана уравнением
задана уравнением ![]() .
.
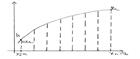
 Разобьем промежуток
Разобьем промежуток ![]() на
на ![]() частей
точками
частей
точками ![]() . Проведя через каждые две
последовательные точки деления дуги хорды
. Проведя через каждые две
последовательные точки деления дуги хорды
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.