3. Гомотетия в k раз -- линейный оператор ![]() на пространстве L такой, что
на пространстве L такой, что ![]() для любого
для любого ![]()
4. Поворот каждого вектора на плоскости на угол a относительно начала координат. Обозначим
этот оператор через ![]() . Линейным оператором будет также
поворот каждого вектора трехмерного пространства на угол a относительно оси.
. Линейным оператором будет также
поворот каждого вектора трехмерного пространства на угол a относительно оси.
5. Симметрия каждого вектора плоскости относительно начала координат (≡ гомотетия с коэффициентом -1).
Симметрия каждого вектора плоскости относительно прямой ℓ ,
проходящей через начало координат (обозначаем ![]() ).
).
Симметрия каждого вектора пространства относительно прямой или плоскости.
6. Проекция пространства геометрических векторов на прямую или на плоскость.
Пусть ![]() -- базис пространства L. Рассмотрим
какой-либо линейный оператор
-- базис пространства L. Рассмотрим
какой-либо линейный оператор ![]() . Разложим элементы
. Разложим элементы ![]() по базису
по базису ![]() :
:
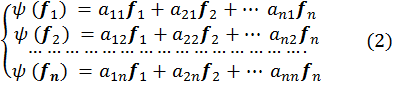
Тогда n× n-матрица![]() будет матрицей линейного оператора ψ относительно
базиса
будет матрицей линейного оператора ψ относительно
базиса ![]() .
.
Предложение. Пусть ![]() –
матрица линейного оператора
–
матрица линейного оператора ![]() относительно базиса
относительно базиса ![]() и
и ![]() -- некоторый элемент. Тогда столбец
координат элемента
-- некоторый элемент. Тогда столбец
координат элемента ![]() в том же базисе равен
в том же базисе равен ![]() .
.
Доказательство.
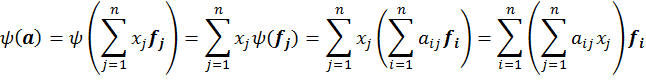
Столбец состоящий из сумм ![]() , где
, где ![]() как раз и совпадает с произведением
как раз и совпадает с произведением ![]() □
□
Заметим, что i-ая строка коэффициентов в разложении (2) ставится на место i-го столбца матрицы A.
Примеры матриц геометрических линейных преобразований плоскости
1. Поворот плоскости на угол ![]() в
стандартном базисе имеет матрицу
в
стандартном базисе имеет матрицу
![]()
2. Гомотетия c коэффициентом
![]() в любом базисе имеет матрицу
в любом базисе имеет матрицу ![]()
3. Проекция плоскости на ось ![]() имеет
матрицу
имеет
матрицу ![]() 4. Симметрия плоскости относительно оси
4. Симметрия плоскости относительно оси ![]() имеет матрицу
имеет матрицу ![]()
Пример. Найдем образ вектора ![]() при повороте на
при повороте на ![]() :
:
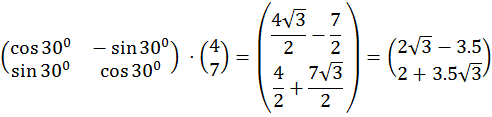
Тем самым образ равен ![]()
В связи с этим возникает естественная задача: найти базис пространства L, в котором матрица заданного линейного оператора ψ имеет наиболее простой вид. Именно к такому классу задач относится проблема диагонализации линейного оператора: найти базис, в котором матрица данного линейного оператора диагональна.
Диагональные матрицы удобны для вычислений. Очень часто для
матричной функции F оказывается, что ![]() . Например, это так , если
. Например, это так , если ![]() -- возведение матрицы в некоторую степень или
-- возведение матрицы в некоторую степень или

-- матричная экспонента.
Пусть ![]() -- линейный оператор линейного
пространства L. Ненулевой вектор
-- линейный оператор линейного
пространства L. Ненулевой вектор ![]() называется собственным вектором оператора
называется собственным вектором оператора ![]() с
собственным числом l , если
с
собственным числом l , если ![]() .
.
Теорема. Пусть A -- матрица линейного оператора
относительно базиса ![]() , и
, и
![]()
Вектор ![]() будет собственным,
с собственным числом l, тогда и только
тогда, когда l является корнем характеристического
уравнения:
будет собственным,
с собственным числом l, тогда и только
тогда, когда l является корнем характеристического
уравнения:
![]()
а столбец ![]() - ненулевое решение следующей однородной
системы линейных уравнений:
- ненулевое решение следующей однородной
системы линейных уравнений:
![]()
Диагонализация линейного оператора в случае простого спектра. Пусть \Aa -- линейный оператор пространства L. Собственные вектора, отвечающие разным собственным числам линейно независимы. Если элементы \f_1,\ldots,\f_n\in L являются собственными, с попарно различными собственными значениями l _1,… ,l _n, и n=dim L то, во-первых, эти элементы образуют базис, а во-вторых, матрица оператора f в этом базисе имеет диагональный вид: \diag(\la_1,\ldots,\la_n).
Доказательство. Достаточно доказать линейную независимость собственных векторов \f_j с попарно различными собственными значениями l _j. Если допустить линейную зависимость вида x_1\f_1+… +x_n\f_n=0 то применяя оператор \Aa к этому соотношению n-1 раз, получим систему
x_1\f_1+… +x_n\f_n=0 x_1l _1\f_1+… +x_nl _n\f_n=0 ........................................................... x_1l _1^{n-1}\f_1+… +x_n\la_n^{n-1}\f_n=0}
Рассматривая эту систему относительно неизвестных x_j\f_j, видим, что ее определитель Вандермонда не равен 0. Следовательно, по правилу Крамара получаем равенства нулю всех x_j\f_j. Так как \f_j≠ 0, то x_j=0 для всех j.□
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.