Линейные и квадратичные функции многих переменных, страница 3

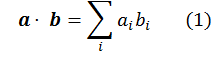
называется (стандартным) скалярным произведением двух строк. Оно удовлетворяет следующим свойствам:

СК1 (билинейность)] .

СК2 (симметричность)]

СК3 (положительная определенность)   и    лишь если .

для любых строк  и l ∈ ℝ .

В общем случае, если на линейном пространстве L задано правило, посредством которого паре  сопоставляется число , удовлетворяющее правилам СК1-СК3, то это правило называется скалярным произведением.

Определение.  Конечномерное линейное пространство L со скалярным произведением  называется  евклидовым пространством. Величину   называют  нормой или  длиной  элемента . Итак, для пространства строк, длина строки  равна . Это совпадает с формулой длины вектора, координаты которого записаны в стандартном базисе.

Неравенство  Коши-Буняковского-Шварца.  Для любых двух элементов  евклидова пространства L имеет место неравенство:

В частности для двух строк выполняется неравенство

Доказательство. Если , то это неравенство тривиально. Иначе рассмотрим квадратный трехчлен . Он принимает только неотрицательные значение в силу свойства СК3.

Следовательно, его дискриминант меньше или равен 0. Получаем . Сокращая на  4,  перенося слагаемое с минусом в правую часть и извлекая квадратный корень, получаем требуемое. □

Углом между ненулевыми элементами  евклидова пространства L назовем  число   такое, что

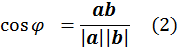
Это определение корректно т.е. число   существует, так как модуль  меньше единицы, что следует из неравенства Коши-Буняковского.

Два элемента пространства со скалярным произведением называются ортогональными (или перпендикулярными в случае геометрических векторов), если либо  один  из них нулевой, либо угол между ними равен π /2. Обозначаем ортогональность так: . Из формулы (2) вытекает критерий  ортогональности:

Элементы  ортогональны тогда и только тогда, когда

Определение. Базис  евклидова пространства L называется ортогональным, если  для всех пар . Если, кроме того, длины всех элементов  равны единице, то этот базис называется  ортонормированным.

Предложение. Стандартный   базис   пространства   строк ортонормирован относительно стандартного скалярного произведения. □

Заметим, что если ненулевые вектора  , евклидова пространства L размерности n, попарно перпендикулярны, то во-первых, они образуют базис пространства L, а во-вторых,  их орты  будут ортонормированным базисом.

Теорема о разложении вектора по ортонормированному базису.  Пусть  -- ортонормированный базис,  и b - какой-либо элемент. Тогда

т.е. i-ая координата разложения элемента b по этому базису равна скалярному произведению .

Действительно, разложение вида существует, ибо  --  базис. Но так как  -- ортонормированный базис, то

Аналогично доказывается равенство  общем случае. □

4.  Линейные операторы

В этом параграфе будет развито достаточно широкое обобщение идеи линейных функций одной и нескольких переменных: , .

Линейным преобразованием пространства строк длины n в пространство строк длины m называется отображение  задаваемое правилом

Если ввести в рассмотрение матрицу  линейного преобразования  и два столбца , , то эту систему можно переписать в виде . Дистрибутивность умножения матриц дает правило . Ясно также, что  для любого числа l . В этих правилах и заключается суть линейности.

Определение 1.  Пусть L и M - линейные пространства. Отображение называется линейным, если ;   для любых элементов  и для  любого  числа l . Если, к тому же, ψ  - биекция, то ψ называется изоморфизмом. В случае  L=M, линейное отображение называем также линейным оператором.

Примеры линейных отображений и операторов

1. Нулевое отображение:  для любого .

2. Единичный оператор  (или просто Id): .