Тригонометрические ряды Фурье

Литература

В.А. Кудрявцев, Б.В. Демидович. Краткий курс высшей математики М., наука, 1989 г

Тригонометрические ряды Фурье

Функция  кусочно-непрерывна на промежутке , если этот промежуток можно разбить на конечное число промежутков, на каждом из которых функция  непрерывна и на частичных промежутках должны существовать односторонние пределы в крайних точках.

Сумма и произведение кусочно-непрерывных функций снова кусочно-непрерывная функция.

Скалярным произведением двух к. непрерывных функций называется число

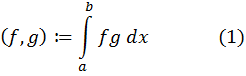
Рассмотрим основную систему тригонометрических функций

общего периода . 

Лемма.   Функции (2) попарно ортогональны на любом отрезке длины .

Доказательство. Используются тригонометрические формулы

Так как

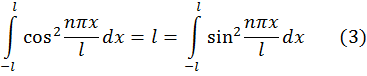
то  система

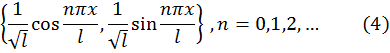
будет ортонормированной.

Пусть  - кусочно-непрерывная периодическая с периодом . Как представить эту функцию в виде суммы  тригонометрического ряда Фурье?

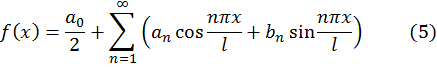
Ответ

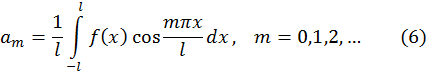
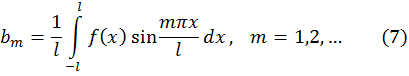
Функции   соответствует ряд Фурье  , где  вычисляются по формулам (6), (7). Когда его сумма  существует и когда эта сумма равна ?

Теорема сходимости. Пусть периодическая функция , определенная всюду, кроме точек разрыва и имеющая период  является кусочно гладкой. Тогда

1) ее ряд Фурье сходится  в любой точке;

2) сумма ряда Фурье равна функции в любой точке непрерывности, а в точке разрыва имеет место равенство

Замечание. Формулы (5)-(7) упрощаются, если

Ряды Фурье четных и нечетных функций

Имеет место формула

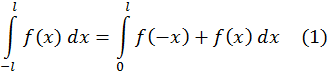
отсюда следует

1) если  четная функция, то

2) если  -- нечетная функция, то

Теорема. Ряд фурье четной функции содержит только косинусы (включая свободный член), а ряд Фурье нечетной функции содержит только синусы.

Примеры разложений на отрезке  по синусам и по косинусам

Ряды Фурье непериодических функций

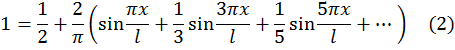
Кусочно-гладкую функцию, заданную на полупериоде можно разложить в ряд Фурье по синусам или по косинусам, продолжая ее по нечетности и по четности на весь период

Пример

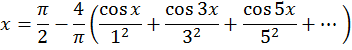
Полагая  получим ряд  Эйлера

Уклонение в среднем.

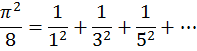
Обозначим через Φ  линейное пространство периодических с периодом 2π , кусочно-монотонных функций таких, что f(x)={1\over2}(f(x+0)+f(x-0)  для любого x. Определим на этом пространстве скалярное произведение

Величину

называют       уклонением в среднем функции f от функции g.

Рассмотрим в Φ  подпространство

тригонометрических многочленов степени ≤  n. Поставим и решим следующую задачу: для данной функции f∈ Φ   найти такой, что среднее уклонение |f-s| имеет наименьшее возможное значение. Пусть

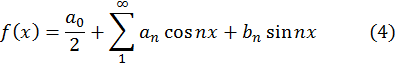
разложение в ряд Фурье. Тогда, как мы знаем

Рассмотрим частичную сумму ряда (4)

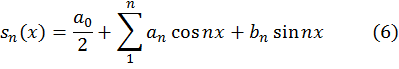
Тогда .

Теорема.   Функция  - решение поставленной выше задачи

Следствием соотношения (*) является   неравенство Парсеваля

      Таблица разложений в ряд Фурье некоторых функций

1.

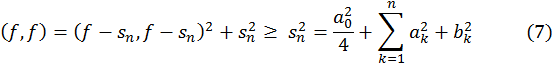
на интервале (-π ,π ). В частности, при x=π /2 имеем:

откуда

2

3

4

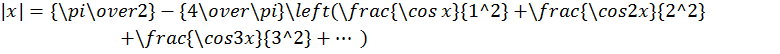
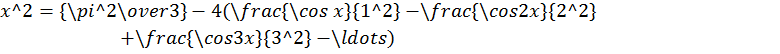
Все эти разложения имеют место на интервале (-π ,π ), на всю числовую ось продолжаются по периодичности.

Функцию, для которой каждый отрезок можно разбить на конечное число подотрезков на каждом из которых эта функция монотонна и непрерывна, а в точках "состыковки" допускаются лишь разрывы первого рода, назовём кусочно-монотонной.