ОДЗ, линии уровня, графики. Области. Предел. Непрерывность

1  ОДЗ, линии уровня, графики

Построить линии уровня 1,-1,1/2,-1/2,0 функции

Построить линии уровня 1, 0, -1 функции z=1-|x|-|y|

Нарисовать линии уровня функций  а) б)  ; в)  z=1-|x|-|y|

Найти и изобразить на плоскости ОДЗ  следующих функций а) ; б) ; в) ; г)

Доказать, что функция  принимает любые значения

2  Области. Предел. Непрерывность

Нарисовать область  на плоскости. Будет ли она а) ограниченной, б) замкнутой, в) открытой, г) связной? Будет ли точка  внутренней (внешней, граничной) для ?

Нарисовать область  на плоскости. Будет ли она а) ограниченной, б) замкнутой, в) открытой, г) связной? Будет ли точка  внутренней (внешней, граничной) для ?

Найти точки разрыва функции . Найти предел  при условии а) ;  б)

(*) Найти предел а)  , б)

3  Частные производные

Найти частные производные функции

Показать, что функция  удовлетворяет  уравнению теплопроводности ( -- температура стержня в точке  в момент t.)

Показать, что функция , где r --расстояние от точки (x,y,z) до начала координат, является гармонической, т.е.  удовлетворяет  уравнению Лапласа

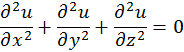
Показать, что функция  удовлетворяет  уравнению колебаний

при любом значении параметра ( -- отклонение точки P(x) струны от горизонтального положения в момент времени  t.)

Найти , если a) ,  b) 

(*) Вычислить якобиан перехода к полярным координатам (r,φ), если x=r cos𝜑; y=r sin𝜑.

(*) Вычислить якобиан перехода к сферическим координатам (r,φ ,θ ), если x=r cosθ cos𝜑; y=r cosθ sin𝜑; z=r sinθ.

Найти касательную плоскость и нормальный вектор к графику функции   в точке .

Найти касательную плоскость и нормальный вектор к  поверхности   в точке .

(*) На поверхности  найти точки, в которых касательные плоскости параллельны координатным плоскостям.

(*) На поверхности  найти точки, в которых касательные плоскости параллельны плоскости  4x+y+2z+9=0

Найти производную по направлению вектора функции  в точке Р(-1,1,2). Найти градиент этой функции в точке Р.

Найти производную по направлению вектора функции  в точке Р(1,-1,1). Найти градиент этой функции в точке Р.

4  Дифференциал

Найти дифференциал функции   в точке A(3,4)

Найти полное приращение функции  при x=2, y=3 как функцию от .

Найти полное приращение и дифференциал функции  в точке a=2, b=1. Вычислить эти величины при условии

Найти , где . Имеет ли функция f стационарные точки?

Вычислить приближённо

В усечённом конусе радиусы оснований -- 20 см, 10 см., а высота – 30 см. Как приближённо измениться объем конуса, если увеличить на 2мм радиусы и на высоту уменьшить на 1 мм?

Найти дифференциал второго порядка функции z=arctg(x/(x+y))

5  Экстремумы, наибольшее и наименьшее значения

Найти наибольшее и наименьшее значения функции   в области 2≥ x≥ 0, 2≥ y≥ 0.

Найти наибольшее и наименьшее значения функции  в области

Найти наибольшее и наименьшее значение функции z=sin x+sin y+sin(x+y) в области 0≤  x≤  π/2; 0≤  y≤  π /2

Найти наибольшее и наименьшее значение функции  в ограниченной замкнутой области, задаваемой прямыми x=0, y=0,  x+y=6

Найти наибольшее и наименьшее значение функции в круге

Найти экстремумы функций  а) z=xy+50/ x+20/y (x>0,y>0) б)   ,(x>0,y>0) в) 

Найти экстремумы функции , заданной неявно соотношением .

Найти экстремумы функции трех переменных

6  Условные экстремумы

Найти экстремум функции z=xy при условии x+y=1

Найти  экстремум функции z=x+2y при условии  Дать геометрическую интерпретацию результата.

Найти  экстремум функции u=x-2y+2z при условии .  Дать геометрическую интерпретацию результата.

Найти прямоугольный параллелепипед заданной площади полной поверхности S,  имеющий наименьший объем.

Найти прямоугольный параллелепипед данного объема V,  имеющий наименьшую площадь полной поверхности

Русла двух рек в пределах некоторой области приближенно представляют параболу  и прямую x-y-2=0. Требуется соединить данные реки прямолинейным каналом  наименьшей длины. Через какие точки его провести?

Определить наружные размеры закрытого ящика с заданной толщиной стенок δ  и внутренней ёмкостью V так, чтобы на его изготовление было затрачено наименьшее количество материала.

Если в электрической цепи с сопротивлением R течёт ток I, то количество тепла, выделяющегося в единицу времени пропорционально I²R. Определить, как следует разветвить ток I на токи  при помощи n проводов, сопротивление которых равны  так, чтобы выделение тепла было наименьшим.

7  Формула Тейлора

Разложить функции а) ;  б)   по формуле Маклорена до членов третьего  порядка включительно. Найти первый, второй и третий дифференциалы этой функции в О(0,0).

ДОПОЛНИТЕЛЬНЫЙ МАТЕРИАЛ

Рассмотрим кривую  

Левую часть (1) обозначим F(x,y). Имеем, во-первых, что биссектрисса 'y=x' - подмножество кривой γ. Далее,

Особые точки кривой γ  - это точки (x,y), удовлетворяющие системе уравнений

Нетрудно из первого и второго уравнения (2) получить, что y∈ {0;1} и, аналогично, x∈ {0;1}. Отсюда получаем, что O(0,0) и P(1,1) - единственные особые точки.

Кривую γ  можно посмотреть в файле x2ey2.mws, но именно в особых точках Maple не дает удовлетворительной прорисовки даже при большом увеличении.

Доказать, что множество целых чисел ℤ   образует метрическое пространство относительно метрики , где  -- наибольшая степень двойки, делящая разность n-m.   Доказать, что последовательность 2,4,8,16,... сходится к 0.

Доказать, что множество ℝ² строк длины 2 относительно линейной метрики

будет метрическим пространством. Для точек O(0,0), A(2,3) найти все точки B(x,y) такие, что ρ₁(O,A)=ρ₁ (O,B)+ρ₁ (B,A) и изобразить их на плоскости. Решить те же задачи для стандартной метрики

Проверить, что линейное пространство C[a,b] непрерывных функций на отрезке [a,b] относительно равномерной метрики

будет метрическим пространством. Пусть выше a=0, b=1. Доказать, что последовательность функций  сходится поточечно к разрывной функции (какой?), но не имеет предела в пространстве C[0,1].