ОПЕРАЦИОНОЕ ИСЧИСЛЕНИЕ
Комплекснозначную функцию действительного переменного f(t) назовем оригиналом, если
1) f(t)=0 при t<0;
2) на каждом отрезке функция f(t) допускает лишь конечное
число особых точек, в которых могут быть лишь разрывы первого рода, в остальных
точках 
удовлетворяет условию Гельдера:
3) найдутся вещественные константы M>0, a такие, что выполняется неравенство |f(t)|≤ Meat для всех t.
Назовем
функцией Хэвисайда. Она будет оригиналом. Задавать оригинал аналитическим выражением мы будем только для t≥ 0. Например, оригинал sin t на самом деле означает функцию равную (sin t)⋅ χ (t), которая совпадает с sin t только при t≥ 0.
Заметим, что из наличия производной в точке t следует
условие Гельдера с 
и любой константой 
, если функция кусочно-дифференцируема и
допускает лишь разрывы первого рода и удовлетворяет условиям 1) и 3), то она
будет оригиналом.
Предложение. Оригиналы образуют линейное пространство.
Изображением оригинала f(t) назовем комплекснозначную функцию
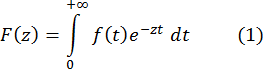
комплексного переменного z.
Предложение. Изображение аналитично в полуплоскости
Re z>a и
.
Интеграл (1) называется преобразованием Лапласа функции f(t).
Этот факт будем записывать как Lap(f)=F(z) или f(t)
F(z)
или F(z)
f(t).
Имеем:
Теорема. Если функция является
оригиналом и 
, то в любой точке t, где выполняется
условие Гельдера, справедливо равенство
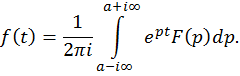
Здесь 
-- любое число, большее чем a (f).
В частности
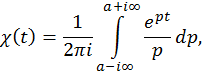
где -- любое положительное число.
Замечание. Интегралы здесь берутся в смысле главного
значения, т.е. как предел интегралов вида 
при b→ +∞ .
Следствие. Если Lap(f)=Lap(g) для оригиналов f и g, то f и g совпадают во всех точках, где соблюдается условие Гельдера.
Отображение Lap линейно:
Как следствие (2), §1 и линейности получаем:
Если Lap(f(t))=F(z) и 
, то Lap(f(bt))=1/b F(z/b )
Доказательство. 
Если 
оригиналы и 
, то
f(n)(t) 
znF(z)-zn-1f(0)-zn-2f'(0)-… -f(n-1)(0)
В частности, если f(k)(0)=0 при k=0,1,2,… , n-1, то f(n)(t) znF(z).
Доказательство.
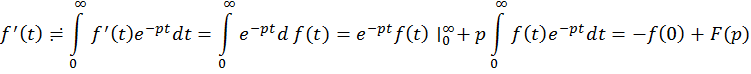
Если Lap(f)=F(z), то F(n)(z) 
(-t)n f(t).
Доказательство.......
Пользуясь этим свойством и исходя из равенства Lap(χ )=1/z, получаем
t^n n!/z^{n+1}; t sin ωt 2zω/(z^2+ω^2)^2;
t cos ωt {z^2-ω^2}/{(z^2+ω^2)^2}
Если f(t) F(z), то ò _0^t f(s) ds F(z)/z
Доказательство………
Если f(t) F(z) и f(t)/t -- оригинал, то
f(t)/t ò _z^∞ F(ζ ) dζ
где [z,∞ ) -- горизонтальный луч, принадлежащий полуплоскости Re z>a (f).
Доказательство.........
Найдем изображение интегрального синуса
si( t)=ò _0^t sin τ/τ dτ :
sin t/t ò _z^∞ dζ /{1+ζ^2}=π /2- arctg z, откуда si
(t) 1/z(π /2-arctg z)
Если Lap(f)=F(z), то Lap(f(t-t_0))=e^{-t_0z}F(z)
Доказательство.........
Примеры. 1) Изображение ступенчатой функции h(χ (t)+χ (t-τ )+χ (t-2τ )+… ) равной nh, если 
есть
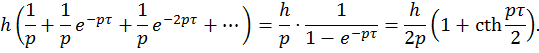
2) Периодический прямоугольный импульс
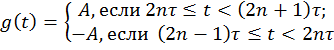
можно записать в виде 
. Следовательно, по теореме запаздывания
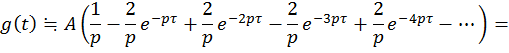
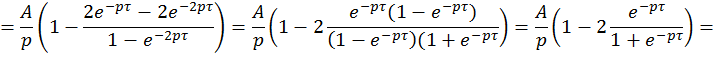
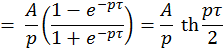
3) Периодический треугольный импульс 
по свойству 5 – интегрирование оригинала
имеет изображение 
F(z), то f(t)e^{at}
F(z-a).Пример. e^{at}
sin ωt \frac{ω}{(z-a)^2+ω ^2}, e^{at}cosω t 
frac{z-ω }{(z-a)^2+ω^2}
Для двух функций f и g обозначим через 
их свертку, т.е. функцию такую,
что
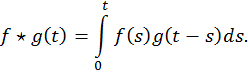
Предложение А. Свертка оригиналов есть оригинал.
Доказательство…………..
Предложение Б. Свертка симметрична и дистрибутивна по отношению к сложению.
Доказательство…………
Теорема (Э. Борель) . Если Lap(f)=F(p) и Lap(g)=G(p), то Lap(
.
Доказательство.
Изображение свертки есть интеграл 
. Это
двойной интеграл по области, изображенной на рис.
Поменяем пределы интегрирования. Получим
t 
Рис. Область интегрирования. 
□
Следствие А. Имеет место гомоморфность 
Следствие Б. (интеграл Дюамеля)
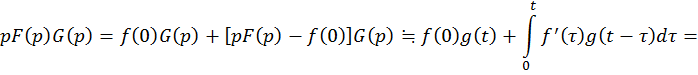
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
