Первая теорема разложения. Пусть F(z) -- аналитична в бесконечности и равна 0 там. Это значит, что ее разложение в ряд Лорана в бесконечности имеет вид F(z)=∑ _1^∞ c_n/z^n. Тогда
f(t)=∑_0^∞ c_{n+1}/n! t^n
Вторая теорема разложения. Пусть F(p)
1) мероморфна и аналитична в некоторой полуплоскости Re
p>![]() ;
;
2) существует система окружностей ![]() ,
, ![]() на которой F(p) стремится к нулю равномерно относительно arg p;
на которой F(p) стремится к нулю равномерно относительно arg p;
3) для любого ![]() абсолютно сходится интеграл
абсолютно сходится интеграл ![]() .
.
Тогда оригиналом F(p) служит функция
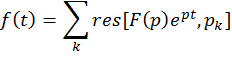
где сумма вычетов берется по всем особым точкам ![]() функции F(p) в порядке неубывания их модулей.
функции F(p) в порядке неубывания их модулей.
Следствие. Если ![]() -- правильная дробь, то ее оригинал есть
-- правильная дробь, то ее оригинал есть
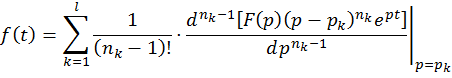
где ![]() -- полюсы
-- полюсы ![]() , а
, а ![]() -- их кратности. В частности если все
полюсы простые, то
-- их кратности. В частности если все
полюсы простые, то
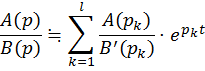
Если в добавок многочлены ![]() имеют действительные коэффициенты, то
имеют действительные коэффициенты, то
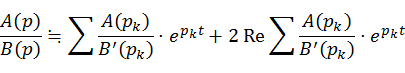
где первая сумма распространяется на действительные полюсы, а вторая на полюсы с положительными мнимыми частями.
Теорема. Пусть f(t,a ) -- зависит от параметра a. Тогда ∂(Lap(f))/∂a =Lap( ∂f/∂ a).
Теорема. Если Lap(f)=F(z), то а) ![]() ;
;
б) ![]() (если эти пределы существуют), в) f(0+0)=limz→
∞zF(z).
(если эти пределы существуют), в) f(0+0)=limz→
∞zF(z).
Обозначим через ![]() линейное пространство комплекснозначных, бесконечно
дифференцируемых функций равных 0 вне какого-либо отрезка.
линейное пространство комплекснозначных, бесконечно
дифференцируемых функций равных 0 вне какого-либо отрезка.
Определение. Семейство функций ![]() назовем дельтообразным при
назовем дельтообразным при ![]() , если
, если
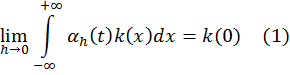
для всякой функции ![]()
Пример. 1) ![]() -- дельтаобразное семейство. При
-- дельтаобразное семейство. При ![]() получаем
обобщенную дельта функцию Дирака
получаем
обобщенную дельта функцию Дирака ![]() равную нулю всюду кроме
точки 0, где она равна +∞ и интеграл от этой функции по ℝ равен 1. Ее изображение
будет 1.
равную нулю всюду кроме
точки 0, где она равна +∞ и интеграл от этой функции по ℝ равен 1. Ее изображение
будет 1.
2) ![]()
Более точно -- это функция δ (t)
имеющая свойство òℝ δ (t)f(t) dt=f(0) для любой непрерывной
функции ![]() . Иными словами дельта функция Дирака есть
линейный функционал на пространстве всех функций из
. Иными словами дельта функция Дирака есть
линейный функционал на пространстве всех функций из ![]() полученный как предел линейных
функционалов
полученный как предел линейных
функционалов ![]()
Предложение. δ (t)=χ (t)' в том смысле, что òℝ δ (t)f(t) dt=ò
ℝ f(t) dχ(t) для любой ![]() . (Последний интеграл понимается в смысле
Стилтьеса)
. (Последний интеграл понимается в смысле
Стилтьеса)
Итак, изображение дельта-функции Дирака есть 1, что
согласуется с правилом дифференцирование оригиналаТогда. ![]() в соответствии с теоремой запаздывания.
в соответствии с теоремой запаздывания.
Импульсные функции высших порядков.
Пусть
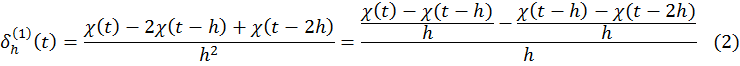
Для функции из ![]() правая часть в (2) в пределе при
правая часть в (2) в пределе при ![]() дает
вторую производную. Найдем изображение оригинала
дает
вторую производную. Найдем изображение оригинала ![]() ерейдем к пределу при
ерейдем к пределу при ![]() .
Получим
.
Получим
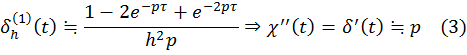
Аналогично
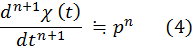
|
ОРИГИНАЛ |
ИЗОБРАЖЕНИЕ |
|
δ (t) (функция Дирака) |
1 |
|
χ (t) |
1/z |
|
|
|
|
|
|
|
|
|
|
|
|
Пример. Решим задачу Коши f(0)=1, f'(0)=0 и f''=f'+f. Обозначим Lap(f)=F(z). Тогда
Решим уравнение
![]()
Операторное уравнение имеет вид
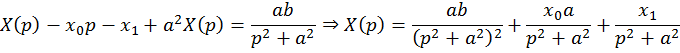
Так как ![]() , то по теореме интегрирования оригинала
имеем
, то по теореме интегрирования оригинала
имеем
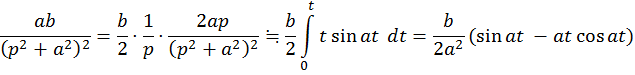
Окончательно,
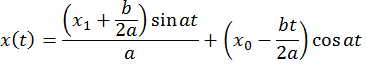
Пример
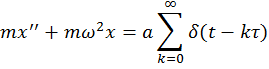
Операторное уравнение имеет вид
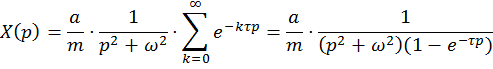
и в предположении, что нет кратных полюсов, получаем
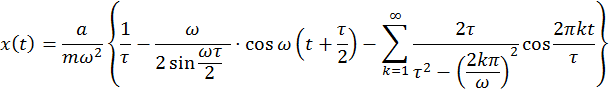
Пусть требуется решить ![]() -- лин. диф. уравнение с правой часть. Пусть
-- лин. диф. уравнение с правой часть. Пусть
![]() его операторный вид. Решим его сначала с
единичной правой частью
его операторный вид. Решим его сначала с
единичной правой частью
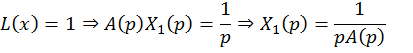
Тогда
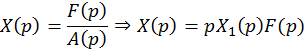
и
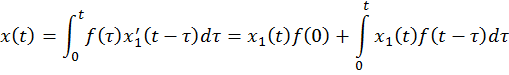
Пример. Решить ![]() Решаем сначала
Решаем сначала ![]() , откуда
, откуда
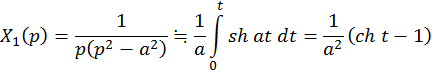
Тем самым
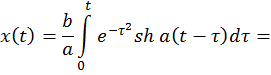
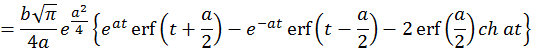
(По определению ![]()
![]()
Пример. Решить систему
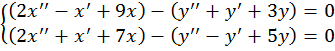
при начальных условия ![]() . переходим к оператоторной системе
. переходим к оператоторной системе
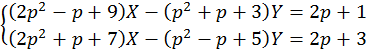
Сумма и разность этих уравнений дает
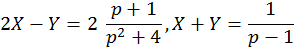
Отсюда
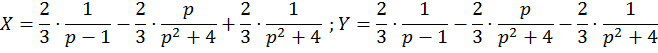
Перейдем к оригиналам
![]()
![]()
![]()
![]() R
L C
R
L C
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
u(t),i(t) u(t),i(t) u(t),i(t)
![]()
![]()
![]()
![]()
![]()
![]()
При ![]() и
и ![]() еще проще—
еще проще—![]() , где
, где ![]() – операторное
сопротивление (импеданс) разное в трех разных случаях
– операторное
сопротивление (импеданс) разное в трех разных случаях
Последовательная схема соединения двух приборов дает
![]()
Параллельная схема соединения приборов дает
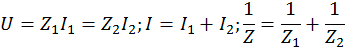
Например в случае последовательного соединения сопротивления, емкости и самоиндукции (RLC-контур) получим
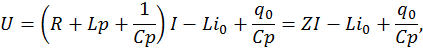
где ![]() – операторное сопротивление контура
– операторное сопротивление контура
Первый закон Кирхгофа – ![]() в любой точке ветвления.
в любой точке ветвления.
Закон ![]() для любого разбиения цепи на
последовательные участки.
для любого разбиения цепи на
последовательные участки.
Роль интеграла Дюамеля – решаем задачу обсчета контура для ![]()
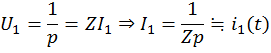
Для произвольной эд.с ![]() и ее изображения U имеем
и ее изображения U имеем
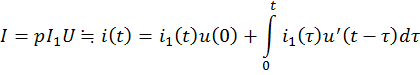
Временная связь ![]()
Пример
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.