Создание частотного радиодальномера с цифровым анализатором спектра сигнала биений, страница 3

          Для вычисления  заметим, что различие между функциями состоит в том, что фронты функции  смещены относительно соответствующих фронтов функции . Максимальное смещение фронтов составляет . Следовательно, наибольшее значение  достигает, когда разнополярные фронты функции  максимально смещены в противоположных направлениях. Пусть для примера положительный перепад функции  смещен вправо на величину , а отрицательный перепад  влево на такую же величину. Тогда

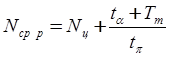
и используя (6) и (7) получим

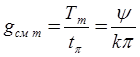
Такой же результат получится и при смещении фронтов в противоположном направлении.

          Максимальная суммарная ошибка

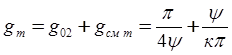
Взяв производную по  и приравняв её нулю, найдем

,

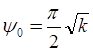при этом

.

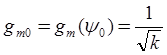            Таким образом, применение дополнительной медленной модуляции позволяет снизить дискретную ошибку измерения  в  раз. Абсолютное значение ошибки измерения дальности при этом не превышает величины :

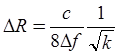
5. Разработка структурной схемы.

Мерой измеряемого расстояния с помощью частотного дальномера является разность частот прямого и отраженного сигналов на выходе смесителя:

 ,                      5.1

которая линейно связана с измеряемым расстоянием:

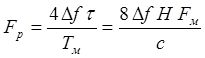.          5.2

    А так как мощность отраженного сигнала  на входе приемника будет

,                    5.3

где - плотность потока энергии отраженного сигнала,

- эффективная поверхность приемной антенны.

    Для случая, когда отражение от диэлектрика происходит по закону зеркального отражения, плотность отраженного сигнала будет

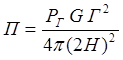  ,                       5.4

где - мощность генератора,

- коэффициент усиления передающей антенны,

- коэффициент отражения.

    Следовательно,    мощность       отраженного     сигнала    будет

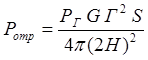                          5.5

    В соответствии с ТЗ, отражающей средой является диэлектрик с диэлектрической проницаемостью . Так как измерения расстояния до плоской поверхности, то . Тогда коэффициент отражения:

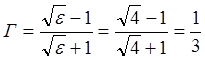.               5.6

В случае нормального падения волны на гладкую идеальную поверхность, последнюю можно заменить зеркально расположенным точечным отражателем. Если учесть потери при отражении на границе с реальной средой, учитываемой коэффициентом отражения по мощности , то плотность потока мощности на расстоянии 2Н на входе антенны:

,

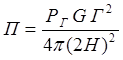где 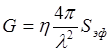 - коэффициент усиления передающей антенны,

где 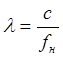 -  длина волны излучаемого сигнала,

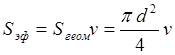 - эффективная площадь зеркальной                                                                                                                    антенны с диаметром ,

- коэффициент полезного действия

тогда                              

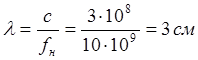
где - скорость света,

- несущая частота (дано в ТЗ);

,

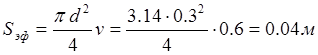где - коэффициент использования раскрыва  антенны .

.

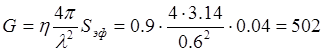Чтобы найти мощность генератора , надо знать мощность отражённого сигнала  формула (5.5), а мощность отражённого сигнала должна быть такой:

,                                     5.7

где   - мощность шума антенны

    Мощность шума антенны  равна:

,                                5.8    

где  - постоянная Больцмана,

 - ,

 - температура антенны,

 -

- эффективная полоса пропускания приемника,

    Так как известны все параметры мощности шума антенны, кроме эффективной полосы пропускания приемника, а она вычисляется следующим образом:

,

где  вычисляется из формулы 5.2

,

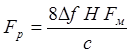где  - девиация частоты,

 - диапазон измеряемых дальностей,

    Для нахождения девиации частоты используем формулу[21]:

,

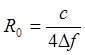где  - погрешность отсчета .

    Следовательно

.

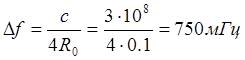Современные генераторы на диоде Гана способны вырабатывать сигналы с ЧМ  для девиации частоты  в достаточно большом диапазоне частоты  модуляции – от долей герц до сотен герц. Для дальнейших расчётов частота модуляции выбрана равной :

    Тогда частота разностного сигнала (5.2)

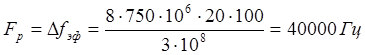
    Отсюда следует, что мощность шума антенны равна (5.8):

.

    Так как следует из формулы (5.7) мощность отраженного сигнала будет:

.

    Тогда мощность генератора равна:

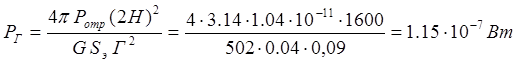Квантование сигнала по уровню вносит в сигнал аддитивным образом дополнительные шумы, уменьшая входное отношение сигнал/шум (ОСШ). Однако с увеличением разрядности квантователя   дисперсия шума уменьшается:

    Получить спектр оцифрованного сигнала можно с помощью дискретного преобразования Фурье (ДПФ):

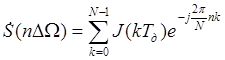,                          5.9

где 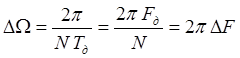                                                                5.10

             - интервал между полученными отсчётами спектра,                                                                              

   - количество отсчётов как временных, так и частотных.

    При цифровой обработке сигнала необходимо учитывать конечность объёма временных выборок. Для ДПФ следствием этой особенности является “размытие”  спектральных составляющих. Вид “размытия” определяется видом выделяющей функции, на отсчёты которой домножаются отсчёты сигнала перед ДПФ. Существует много различных выделяющих функции.

    При наложении на гармонический сигнал (рис.5.1а), спектр которого изображён на (рис.5.1б), прямоугольной выделяющей функции (рис.5.1в,д) вид “размытия” спектра (рис.5.1г,е, соответственно), а точнее огибающая спектра изменяется по закону . При наложении на это же колебание выделяющей функции треугольного вида (рис. 5.1ж) огибающая спектра (рис.5.1з) изменяется по закону  и будет иметь меньший уровень боковых лепестков.

Итогом ДПФ (5.9) является последовательность из отсчётов спектра, взятых с дискретностью (5.10). При отсутствии сдвига последовательности ДПФ её первый отсчёт соответствует нулевой частоте, второй ,третий и т.д., последний .

    Из-за дискретности преобразования центральная частота огибающей спектра сигнала с конечным объёмом выборки, соответствующая частоте периодического сигнала (рис.5.1а),совпадает с i-ой частотной выборкой только в случае кратности  дискрету :

,

где i – целое число.

Из (рис.5.1г,е,з) видно, что по положению спектральной линии, имеющей максимальную амплитуду, можно определить частоту сигнала (рис.5.1а) с точностью .