Создание частотного радиодальномера с цифровым анализатором спектра сигнала биений, страница 2

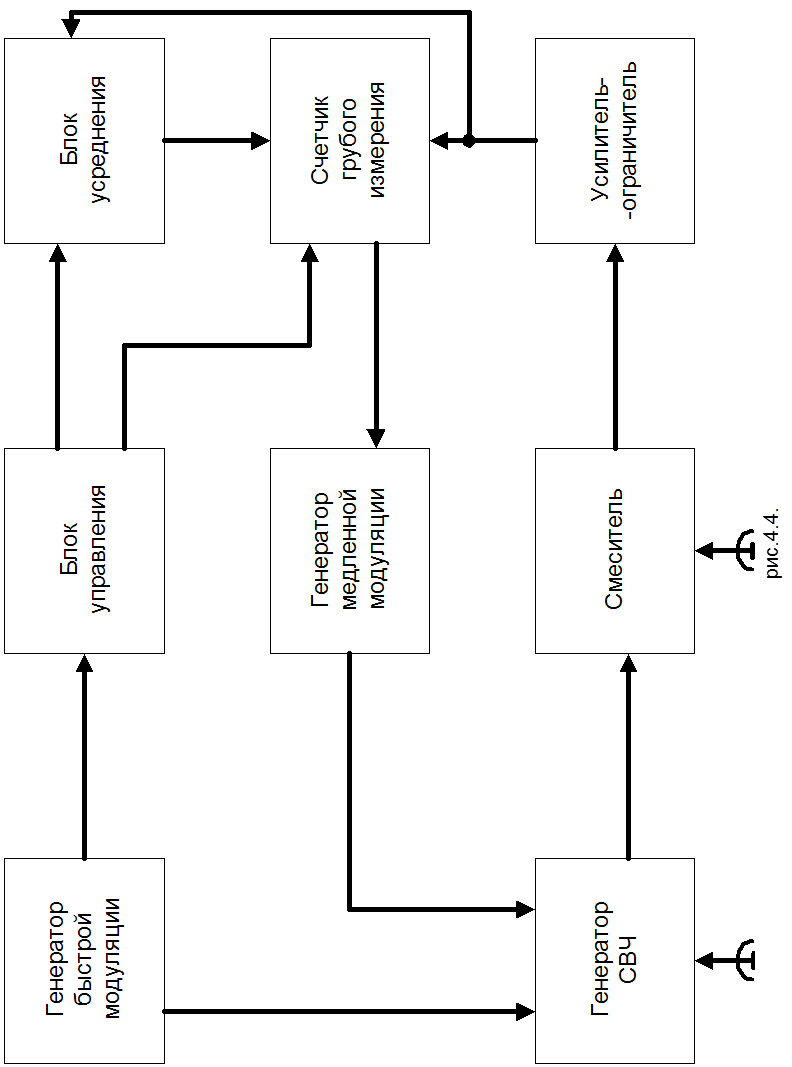
    Будем считать, что несущая частота передатчика изменяется по закону

                                       4.1

 где      - некоторое постоянное значение;

 - быстрая модуляция несущей частоты передатчика;

- медленная модуляция несущей частоты;

    С принципиальной точки зрения закон быстрой модуляций может быть любой периодической функцией времени: синусоидальной, пилообразной, треугольной и т. д.

    Для определенности будем считать, что он имеет симметричную треугольную форму с периодом , так что для одного периода справедливо соотношение:

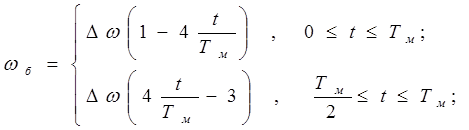
где      девиация частоты при быстрой модуляции.

    Медленная модуляция осуществляется по линейному закону 

 , ,

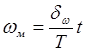где   - максимальное смещение несущей частоты за счет медленной модуляции;

Т - интервал усреднения, причем

где к- целое и

    Сигнал биения на выходе смесителя определяется выражением:

где       - фаза сигнала биения.

    Будем      рассматривать      случай,          когда        ,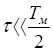

где      задержка отраженного сигнала.

    В этом случае фаза сигнала биений определяется соотношением

или с учетом (1)

     Графическое изображение фазы биений показано на рис.4.5а Горизонтальные линии на графике соответствуют значениям

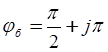,         j= 0,1,2,3…

    При этих значениях фазы сигнала биений пересекает линию нулевого уровня. Обозначим через N - число нуль - пересечений в сигнале биений на

интервале монотонности функции  (в дальнейшем интервал будем называть полупериодом)

    Информация о задержке сигнала заключена в параметре , предоставляющем собой диапазон  изменения фазы биений за счет быстрой модуляции

,

откуда   ,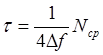

где          ;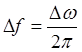

.

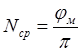    Физически величина   выражает среднее число нуль - пересечений за полупериод. В качестве измеряемого параметра удобно рассматривать не , а величину , так как в этом случае погрешность измерения

где       - оценка параметра ,   

не посредственно показывает степень подавления дискретной ошибки по отношению к дальномеру без дополнительной медленной модуляции, поскольку в последнем максимальная величина этой ошибки равна 1.

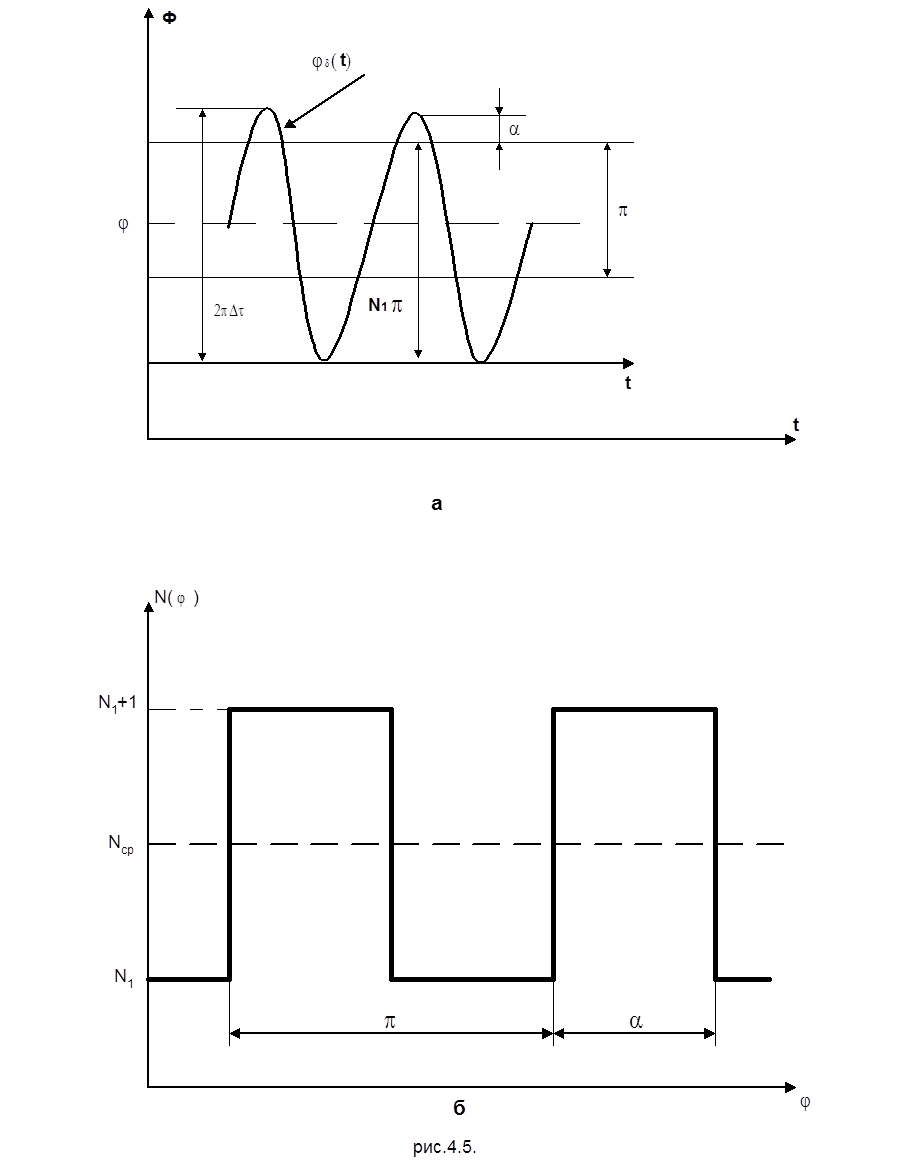
    Обозначим индексом i – номер полупериода ,             

где  ,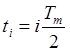

i =1,2…2к, символом   - число нуль - пересечений на i-ом полупериоде.

    Изменение переменной  от времени показано на рис.4.5б. Каждый отсчет  соответствует окончанию i-го полупериода и таким образом (t) представляет собой функцию дискретного времени. Функция  принимает всего лишь два значения:  и , где  - целая часть . Оценкой параметра считается среднеарифметическое значение всех  отсчетов  на интервале усреднения Т

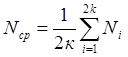                                     4.2

    Вместо функции дискретного времени (t) введем эквивалентную ей в смысле среднего значения функцию непрерывного времени , которая на каждом отдельно взятом полупериоде определена как

.

    Эту функцию можно считать периодической с периодом  отклонение от периодичности возникает за счет ее дискретности.

     Тогда формула (4.2) заменится новым выражением

.

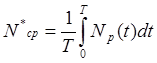    Задача состоит в определении ошибки измерения      

,

которая складывается из двух ошибок – дискретизации и усреднения. В соответствии с этим и задача делится на два этапа.

    1.Заменим реальную функцию , идеальной , которая получается из  путем идеального перехода при :

.

4.        Временные координаты положительных и отрицательных перепадов функции  находятся соответственно из уравнений:

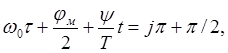
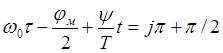,        j=0,1,2…

где                                                                                                    (3)

диапазон измерения фазы биения за счет медленной модуляции. На рис. 1 координаты перепадов соответствуют точкам пересечения огибающей максимумов и огибающей минимумов функции  с горизонтальными линиями.

Функция  является периодической с периодом  и средним значением  ( вычисленным за период ). Нетрудно убедиться, что

                                                (4)

Далее для функции  найдем оценку ее среднего значения

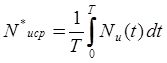                                 (5)

и ошибку усреднения

.

Интервал усреднения Т в общем случае не кратен периоду  и поэтому                              

2. Определим теперь отклонение среднего значения реальной функции  от среднего значения функции

.                                         (6)

Величины слабо связаны друг с другом и могут иметь разную полярность. Поэтому, если интересоваться максимальным значением ошибки g

,

то можно считать, что

где       ,        

    Найдем

С учетом (4) величину  можно выразить через параметры функции

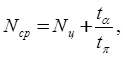                         (7)

где         

 .

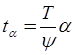
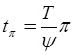
Обозначим приращение фазы сигнала биений за счет медленной модуляции через 

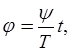                                    (8)                                                                                                

и перейдем от функции  к функции

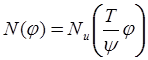
Сделав в (5) замену переменной (8) получим

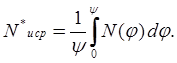
Функция  периодическая, ее период равен . Для вычисления  представим интервал  в виде

где m – целое, положительное число, . При фиксированных m и х погрешность  зависит от  и от сдвига функции N() относительно начала интервала усреднения . Разбив задачу на два случая : , нетрудно убедиться, что в обоих случаях максимальная ошибка одинакова и наступает при  при одновременном совпадении начала интервала усреднения с одним из фронтов функции : если начало интервала усреднения совпадает с положительным периодом ,то имеет место случай , в противном случае .  

4.1.1.      Величина погрешности при этом равна

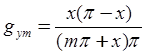
На первом участке (m=0) функция  линейна 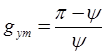. При увеличении  ошибка усреднения уменьшается.

      Уравнение огибающей имеет вид

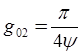
        В реальных дальномерах величина , определяемая (3), известна лишь приближенно. Поскольку неизвестна точно задержка сигнала . Поэтому вместо ошибки усреднения  удобно использовать её огибающую.