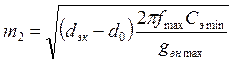Проектирования радиосвязных и радиовещательных приемных устройств индивидуального пользования, страница 8

   , где   ;     ;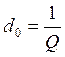

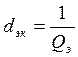g_{вн max} – максимально возможная проводимость следующего каскада приемника; d_0min берется из таблицы 2.2.

Табл.2.2.

Диапазон частот	ДВ	СВ	КВ	УКВ	ДЦВ
d0min	0,01..0,02	0,01..0,02	0,008..0,015	0,006..0,01	0,0003..0,002

Если окажется, что m₂ >1, то необходимо включить добавочное сопротивление последовательно с катушкой

.

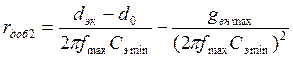Далее проверяется с новым значением m₂ реализуемость минимальной эквивалентной емкости контура. Если данное неравенство не выполняется, то увеличивают С_эmin до значения равного правой части неравенства.

Вводим расчетные коэффициенты.

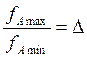; где 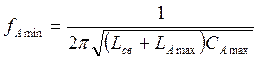; 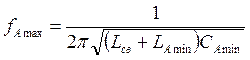, где L_A,C_A – это значения параметров эквивалентной схемы антенны,

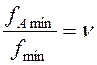,  где f_min – минимальная рабочая частота поддиапазона. Если задаться величиной n, то.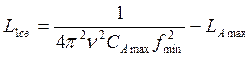

В некоторых случаях сопротивление антенны может иметь индуктивный характер. В этом случае может оказаться, что L_св будет отрицательным. Тогда принимают его равным 5L_Amax , и для последующих расчетов параметр n заменяют другим параметром

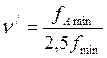
Наибольшее значение коэффициента связи между катушками при допустимой расстройке входного контура

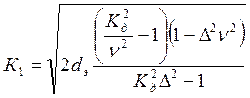, где 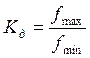 – коэффициент диапазона

Определим наименьшее оптимальное значение коэффициента связи между катушками

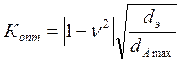, где 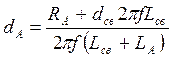 – затухание антенной цепи, d_св = 0,02..0,01 – собственное затухание катушки связи. Расчет коэффициентов выполняется на крайних и средних частотах поддиапазона и в формулу подставляют наибольшее из значений d_А .

Добавочное последовательное сопротивление для первого контура

.

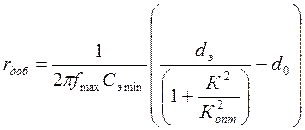Если r_доб < 0 , то это означает, что при выбранных параметрах контура и коэффициенте связи между катушками К нельзя обеспечить принятое в расчете эквивалентное затухание контура.

Требуемое значение собственного затухания контура при r_доб = 0

.

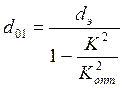Если d₀₁ конструктивно не реализуемо, то принимают его равным наименьшей реализуемой величине. После этого определяют новое максимально допустимое значение коэффициента связи

.

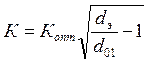Определим эквивалентное затухание контуров в начале диапазона.

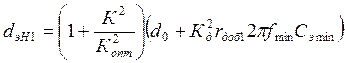 для первого контура,             (1)

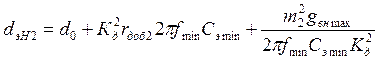 для второго контура.       (2).

В формулы подставляем значение К_опт и входной проводимости следующего каскада на минимальной частоте поддиапазона. Затем находим среднее геометрическое значений затухания контуров для начала диапазона.

.

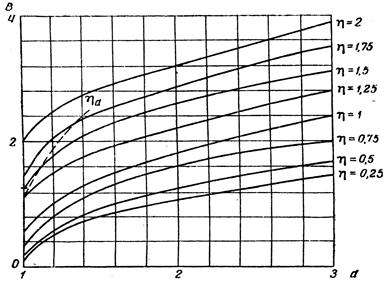   Принимаем для конца поддиапазона параметр связи h_к равным определенному ранее, задаемся величиной d [дБ] неравномерности в полосе пропускания и находим соответствующий ему коэффициент пропорциональный полосе пропускания фильтра B_к. Он находится по графикам Рис.2.7.

Рис.2.7

Определим коэффициент расширения полосы для начала диапазона

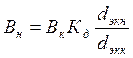, где d_экк эквивалентное затухание контуров в конце диапазона.

По величине B_н и графикам находят соответствующий коэффициент связи h_н в начале диапазона. Если h_н = < h_d , то оба значения параметра связи реализуемы. В противном случае принимают h_н = h_d и по графикам находят соответствующее значение B_н . Затем из предыдущей формулы находят новое значение B_{к .,}  а по графикам – соответствующую величину h_к .

Определим емкости конденсаторов связи

,  .

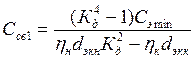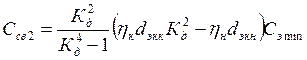Определяем индуктивности катушек контура

, .

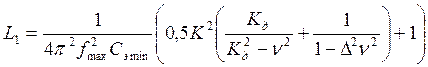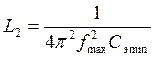Коэффициент передачи входной цепи для крайних и средней частот поддиапазона

.

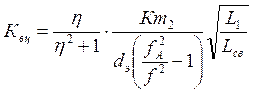Параметр связи на произвольной частоте

.

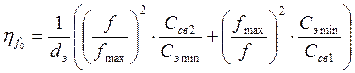Это значение требуется в предыдущей формуле при определении коэффициента на средней частоте. Здесь d_э на частоте f равно среднеквадратическому значению затуханий контуров на этой частоте. Последние вычисляются по формулам (1,2) при замене в них К_д на 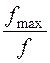 и f_min на f .

Для определения ширины резонансной кривой на заданном уровне ослабления d необходимо воспользоваться формулой  

Для оценки избирательности по зеркальному и соседнему каналам находят соответствующие обобщенные расстройки. Затем по выше приведенным формулам определяют избирательность для этих расстроек.