Системы измерения дальности. Лазерное профилирование, страница 8

Примером типичного спутникового радиолокационного альтиметра служит RA-2, который работает на спутнике Envisat на высоте 800 км. Его рабочие частоты ___________ = 13,6 ГГц и S = 3,2 ГГц. Антенна альтиметра имеет диаметр 1 м, что дает ширину зоны обзора 26 и 90 км для соответствующих рабочих частот. В режиме наибольшего разрешения на частоте Ки система использует импульсы длиной 3,1 не. При этом режим конечного импульса дает ширину зоны обзора 1,7 км. При работе на частоте ____________ используются импульсы длиной 6,3 не. При этом режим конечного импульса дает ширину зоны обзора 2,4 км.

Разрешение дальности при единичном измерении на плоской поверхности равно ctp/2, или около 0,5 м для частоты Ки и 1 м для частоты S. Это разрешение системы улучшают до 5 см для частоты Ки и 20 см для частоты S применением метода усреднения с многократными измерениями. Частота повторных импульсов составляет 1800 Гц, что занимает время 56 мс, за которое спутник относительно Земли перемещается на 400 м. Следовательно, пространственное разрешение составляет 400 м. Корректировка на влияние ионосферы составляет 5 см.

Нужно отметить, что на частоте ________________ альтиметр может работать в двух режимах с низким разрешением с импульсами длиной 12,5 и 50 не. Это дает ширину области обзора 3,5 и 7 км соответственно и разрешение дальности 20 и 75 см соответственно. Эти режимы используются для измерений территорий со сложным рельефом.

В заключение важно отметить, что современные спутниковые альтиметры, несмотря на технические трудности, способны обеспечить точность измерений дальности порядка 10 см. Также важно отметить, что альтиметры используют экстремально короткие импульсы, и, как известно, в них трудно вместить достаточно мощности. Поэтому применяется сжатие импульсов.

8.4. Другие системы измерения дальности

Естественно, кроме лазерных радиометрических альтиметров существуют другие системы измерения дальности. Например, радиосистема эхо-зондирования (см. гл. 1). Принцип работы данной системы основан на измерении времени возврата отраженного сигнала. Такие системы применяются для измерения толщины ледяных покровов и ледников. Обычная рабочая частота таких систем 100 МГц. Так как длина затухания во льдах этой частоты составляет от 100 до 1000 м, то сигнал может проникать на большую глубину льда и система сможет детектировать эхо с глубины несколько тысяч метров. Эта технология успешно применяется для создания карт ледниковых покрытий. В этих системах используются антенны узкого пучка, что накладывает особое требование к высоте, на которой находится спутник.

Аналогичная технология применяется для определения толщины соленого льда, хотя в этом случае более высокая проводимость значительно уменьшает длину затухания. Поэтому системы обладают более высокой мощностью и применяются более низкие орбиты спутников.

Следует отметить радары зондирования почвы, которые используются в археологических исследованиях. Технология, которую применяют такие радары, похожа на технологию эхо-зондирования, но используются микроволновые частоты.

Задачи

1. Система лазерного профилирования работает в диапазоне 1 мкм и на высоте 10 000 м. Угол наблюдения составляет 45° к надиру. Необходимо определить поправку дальности для чистой атмосферы и для атмосферы, количество паров воды в которой составляет 50 мм конденсированной воды. Атмосферное давление на высоте 10 000 м равно 0,26 атмосфер.

2. Получите уравнение (8.14).

3. Лазерный радиометрический альтиметр вырабатывает импульсы, мощность которых изменяется во времени по закону Гаусса, длительность импульса равна 3 не между 1/е точками. Импульсы отражаются от поверхности, рельеф которой подчиняется закону Гаусса, с шириной 1 м между 1/е точками. Необходимо определить время, за которое отраженный импульс набирает от 8 до 92 % своего значения (время нарастания импульса). Эффектом когерентности можно пренебречь. (84 % площади кривой Гаусса находится между 1/е точками.)

4. Сигнал с частотной модуляцией, в котором угловая частота изменяется равномерно от  до  за время Т, можно записать как:

где фаза определяется как:

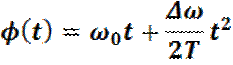
для . Этот сигнал проходит далее через линию задержки, влияние которой на угловую частоту со можно представить умножением на коэффициент:

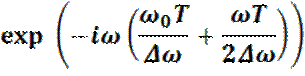
Докажите, что частота сигнала после линии задержки модулирована огибающей с шириной .