Системы измерения дальности. Лазерное профилирование, страница 4

Из рис. 8.11 видно, что принимаемая мощность содержит полезную информацию только в течение периода ____________________________. В более позднее время полезной информации альтиметр не получает. Это означает, что площадь обзора альтиметра — это диск с радиусом ________________:

который является диском рассеивания в момент времени _______________.

При рассмотрении этой модели функционирования альтиметра предполагалось, что ширина луча антенны значительно большая и можно пренебречь отклонениями луча от его оси. На самом деле это не совсем верно: эффект отклонения диаграммы направленности антенны является причиной снижения принимаемой мощности. Следовательно, график на рис. 8.11 должен иметь вид графика на рис. 8.12.

Нужно отметить два момента. Во-первых, пренебречь уменьшением диаграммы направленности антенны можно, если:

В этом случае уравнение (8.9) корректно описывает пространственное разрешение, а альтиметр — это альтиметр с конечным импульсом. Однако если:

то пространственное разрешение равно ______________, а альтиметр — это альтиметр с конечным пучком. Большинство лазерных радиолокационных альтиметров являются альтиметрами с конечным импульсом, в то время как лазерные системы профилирования являются альтиметрами с конечным пучком. В качестве примера рассмотрим лазерный радиолокационный альтиметр с длиной импульса 3 нc, работающий на высоте 800 км. Из уравнения (8.9) получаем, что радиус области обзора приблизительно равен 850 м. Из п. 2.7 известно, что угловая ширина луча антенны с диаметром D на длине волны _______________ приблизительно равна _______________. Тогда, если ____________ = 3 см и D = 1 м, то радиус области обзора будет равен 30 км. В этом случае альтиметр будет с конечным импульсом.

8.3.1. Эффект кривизны Земли

В описании функционирования альтиметра с конечным импульсом использовались некоторые упрощения, которые имеет смысл оценить. Одним из упрощений было признание плоскостности поверхности Земли. Для альтиметров, которые используются в аэронаблюдениях, это вполне допустимо.

Но для космической лазерной радиолокационной альтиметрии это некорректно. А учесть кривизну поверхности Земли очень просто. На рис. 8.13 показано, как рис. 8.9 можно модифицировать для такого учета кривизны. Допустим, Земля — это сфера с радиусом R, тогда из тригонометрии можно записать:

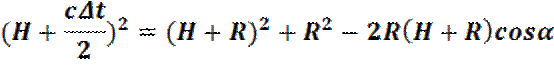
Допустим, _______________, тогда:

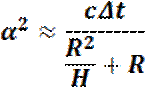
Так как __________________ то:

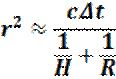
С учетом этой поправки, используя уравнение (8.9) можно вычислить эффективную высоту альтиметра, которая будет равна:

Возвращаясь к примеру, описанному выше (t = 3 не, Н= 800 км), получаем, что эффективная высота прибора составит 11 км.

8.3.2. Поправки на когерентность

Модель функционирования лазерного радиолокационного альтиметра можно улучшить, если аннулировать предположение об изотропности рассеивания поверхностью Земли. Это очень важно, так как принимаемая альтиметром мощность пропорциональна количеству рассеивателей, находящихся в области обзора альтиметра. Поэтому необходимо определить зависимость принимаемой мощности от типа рассеивателей. Если излучение, получаемое антенной от двух рассеивателей, когерентно, сигналы являются помехой друг для друга. Поэтому в анализ вводится понятие вектора (фазора) с определенной амплитудой и фазой.

Две точки будут когерентно по отношению друг к другу излучать мощность, если разница расстояний от точек излучений до источника (альтиметра) меньше, чем длина когерентности Ic, а расстояние между точками, которое измеряется в перпендикулярном к распространению направлении, будет меньше, чем ширина когерентности wc. Эти величины определяются по формулам: