Построение интегральной кривой стока в прямоугольной и косоугольной системах координат для р. Ломпадь. Построение гистограммы и статистической кривой обеспеченности максимальных годовых расходов реки Болва

Санкт-Петербургский Государственный Политехнический Университет

Инженерно-строительный факультет

Кафедра «Гидротехническое строительство»

Курсовая работа

по инженерной гидрологии

           Выполнил: студент  гр.2015/5

                   Азарова Е. С.

          Преподаватель:  Скворцова О.С.

Санкт-Петербург

-2011-

Содержание

I. Построение интегральной кривой стока в прямоугольной системе координат для р.Ломпадь.

II. Построение интегральной кривой стока в косоугольной системе координат для р.Ломпадь.

III. Построение гистограммы и статистической кривой обеспеченности максимальных годовых расходов реки Болва.

IV. Построение математической и эмпирической кривых обеспеченности максимальных годовых расходов реки Болва.

V. Вычисление коэффициента корреляции между максимальными наблюдёнными расходами рек Болва и Ломпадь.

VI. Вычисление параметров математической кривой обеспеченности максимальных годовых расходов реки Ломпадь при удлинении ряда наблюдений до 25 лет.

VII. Нахождение максимальных расчётных расходов для реки Болва при условии строительства гидротехнического сооружения I класс капитальности,для реки Ломпадь- II класса капитальности.

I. Построение интегральной кривой стока в прямоугольной системе координат.

     Основными гидрологическими характеристиками реки являются: отметка уровня поверхности, скорость течения воды ,площадь живого сечения , расход воды Q, Сток W. Важной характеристикой реки является гидрограф. По гидрографу можно определить тип реки, вид ее питания. Пользуются интегральной кривой стока, характеризующей сток реки. Интегральная кривая строится либо в прямоугольной, либо в косоугольной системе координат.

Расход (Q, [м³/с]) – количество воды, проходящей через живое сечение реки в единицу времени.

Сток (W, [м³]) – количество воды, проходящий через живое сечение реки за определённый промежуток времени (обычно один год).

Значение стока за промежуток времени t₁-t₂ можно получить путем интегрирования функции Q =∫f(t), где Q - расход воды, как функция от времени.

Элементарный сток за промежуток времени Δt_i  равен:

ΔW_i = Q_срi ·Δt_i ,

где Q_срi  - среднемесячный расход [м³/с], Δt_i =одному месяцу [с]

Сток за время t_i =n·Δt_i равен сумме n элементарных стоков, т.е. W_i =∑ΔW_i , где n-число месяцев.

Все необходимые расчеты ведутся в табличной форме по среднемесячным значениям расходов Q_i (i=1,2,3,...,n месяцев). Q36 - средний расход за весь период времени.

Из анализа интегральной кривой  в прямоугольной системе координат следует, что тангенс угла между осью абсцисс и касательной к интегральной кривой в данной ее точке равен расходу в данный момент времени в масштабе чертежа.

Свойства интегральной кривой.

1. Функция стока от времени W=f(t) - неубывающая, следовательно первая производная этой функции должна быть ≥  0, т.е. dW/dt ≥ 0.

2. Точка перегиба на кривой стока соответствует либо Q_max, либо Q_min. В точке перегиба функции вторая производная обращается в ноль.

Если вторая производная положительна, то кривая обращена выпуклостью вниз.

Если вторая производная отрицательна, то кривая обращена выпуклостью вверх.

d²/dt²=dQ/dt

Если dQ/dt>0, то расходы увеличиваются, если наоборот, то расходы уменьшаются.

3. Тангенс угла наклона (α) прямой, проходящей через две точки на кривой стока, численно равен среднему расходу за время Δ t_i = t₂-t_1.

tg α =(W₂-W₁)/( t₂-t₁)= Δ W/ Δ t=Q_1-2 - средний расход за время от t₁ до t₂

4. Средний годовой расход можно получить, соединив прямой точки соответствующие началу и окончанию года.

Лучевой график.

Обычно суммарные кривые снабжаются лучевым масштабом, с помощью которого можно определять расходы воды в реке в заданные моменты или промежутки времени. Масштаб снабжается вертикальной осью расходов, при этом полюсное расстояние Р выбирается таким, чтобы осью расходов было удобно пользоваться. Кривая  W=f(t) ,ось t- горизонтальная. Выбрав центр О на горизонтальной прямой, проведём из него пучок прямых под различными углами к этой прямой. Каждому из этих лучей соответствует определённый расход. Этот пучок называют лучевым масштабом расходов (см. лист 1 миллиметровки А3).Точка О - полюс. Р - полюсное расстояние определено по формуле :

ОР=m_qm_t/ m_w   =7,46см

где m - масштабные коэффициенты стока, расхода и времени.

m_t  =2,63*10⁶с/см*ч              m_w  =100*10⁶ м³/см*ч                   m_Q=5*10⁶ м³/см*ч

II. Построение интегральной кривой стока в косоугольной системе координат.

 Суммарная кривая имеет более компактный вид в косоугольной системе координат, особенно, если в качестве одной из осей использовать прямую, которой в прямоугольной системе координат соответствует средний многолетний расход.

Прямую, соответствующую среднему расходу, поворачиваем на угол _о  по часовой стрелке. Эта прямая в новой системе координат станет горизонтальной и принимается осью времени t, а действительная ось времени займёт положение t_о. При построении кривой стока в косоугольной системе координат мы увеличиваем масштаб стока (т.е. уменьшаем масштабный коэффициент), оставив масштаб времени без изменения.

Таким образом при построении кривой стока в косоугольной системе координат необходимо произвести вычисления

ΔW_ik=W_i-W_i

При вычислении величин ΔW необходимо учитывать знак, причем положительные значения откладываем над новой осью t, а отрицательные под нею.

Для того чтобы определить сток в прямоугольной системе координат, например к моменту времени t_i, необходимо восстановить перпендикуляр в этой точке к оси t до пересечения с кривой стока и провести через точку пересечения прямую параллельную оси t_о. Точка пересечения этой прямой с осью W даст величину искомого стока.

Необходимость обращаться каждый раз к оси W, создает неудобства при пользовании такой системой координат. В связи с этим обычно выбирают на оси W величину стока W_о кратную 2, 5, 10, проводят через точку W_о прямую, параллельную оси t_о, определяют расстояние до точки пересечения этой прямой с осью t.

Откладывая на оси t последовательно отрезки 2х, 3х, 4х и т.д., проводим через соответствующие точки линии, параллельные оси t_o. При этом сама ось W становится ненужной. Сток легко определяется путем интерполяции, осуществляемой с точностью, с какой определяется сток при использовании оси W, так как расстояние по вертикали между двумя любыми соседними линиями равно W_o.

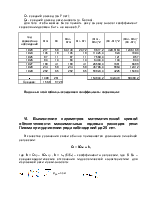
Все данные и вычисления приводится в таблице .

1, 2, 3 и 5 колонки заполняются согласно заданию.

6-я колонка. Сток за месяц определяется умножением расхода на число секунд в месяце (4*5).

7-я колонка. Суммарный сток складывается из суммы стоков всех предыдущих месяцев, т.е. W₁= ∆W₁, W₂=∆W₁+∆W₂, …

8-я колонка. В данной колонке берётся не конкретное значение расхода за каждый месяц, а Qср, которое считается по формуле Q_ср=∑∆W_i/ ∑∆t_i , то есть сумма всей 6-й колонки поделить на сумму 4-й.

9-я колонка. Аналогично 7-у столбцу высчитывается суммарный сток при Q_ср

После этого считается т.н. общая невязка n_общ = W₃₆ – W_ср36 (получается вычитанием последнего, 36-го значения 9-го столбца из 36-го значения 7-го).

Интегральная кривая стока в прямоугольной с.к. строится по 2-й и 7-й колонкам, в косоугольной с.к. – по 2 и 11 или 10 колонкам.