III. Построение гистограммы и статистической кривой обеспеченности максимальных годовых расходов реки Болва.
Хронологический ряд измеренных гидрологических величин представляет простую статистическую совокупность, на основании соответствующей обработки которой можно построить статистический ряд.
В гидрологических расчетах принято использовать нормированные значения величин, которые называются модульными коэффициентами.
Определяем среднее или нормированную величину Q по формуле:
Q=∑Q/n,
где Q – измеренная величина,
n – количество всех встречающихся величин.
По нашим данным получилось:
Q=∑Q/n= 140,24
n(мода)- точка соответствующая максимальному числу появления случайной величины
математ.ожидание (норма)= k( среднеарифметич.)
медиана Mе- проведенная из неё горизонталь делит площадь под кривой на 2-е равные части(соответствует 50% по оси Р).
Находим модульный коэффициент расхода K по формуле:
Ki=Qi/Q
Сначала расставляем значения Qi р.Болва от максимального к минимальному. Находим ∑Qi и Qср. Определив Qср, мы нормируем ряд, норма ряд – Ki=Qi/Qср.
В гидрологических расчётах применяется понятие обеспеченности - Р - вероятность превышения заданной величины. (см табл.2).Если рассматривать набор случайных величин, изменяющихся от kmax=2,03 до kmin=0,24, то можно получить статистический ряд, разбив все значения на ряд интервалов и определить вероятность «попадания» в каждый интервал. Строят гистограмму плотности вероятности случайных величин, а также статистическую суммарную кривую обеспеченности
Число интервалов 
Принимаем количество интервалов N=12.
Определяем величину интервала ∆К=(Kmax – Kmin)/N, при этом мы получаем границы интервалов. Получили 12 интервалов по 1,2см.
Определяем значения модульных коэффициентов на границах интервалов Ks. При совпадении модульного коэффициента Ki из хронологического ряда с Ks на границе двух интервалов условно считаем его принадлежащим предыдущему интервалу;
Подсчитываем количество величин mj из хронологического ряда, попадающих в каждый интервал;
Поделив mj на число наблюденных величин n, получаем относительную частоту;
Затем определяем обеспеченность по формуле:
Pj=∑(mj/n);
IV. Построение математической и эмпирической кривых обеспеченности максимальных годовых расходов реки Болва.
Нам необходимо найти, пользуясь данными наблюдений (эмпирическими), подобрать закон распределения. Для того чтобы подобрать закон распределения, нам необходимо знать следующие величины:
- среднее ряда (среднее значение);
- дисперсию (среднее квадратичное отклонение);
- коэффициенты вариации и асимметрии.
Построение эмпирической кривой обеспеченности.
Рэмп = i/n, где i – порядковый номер наблюдения (уровень или расход) в ранжированном ряду; n – общее число наблюдений.
Рэmax =1/n– обеспеченность, соответствующая максимальному значению.
Рэmin = n/n – обеспеченность, соответствующая минимальному значению (25/25).
Эмпирическая кривая обеспеченности ограничена крайними значениями обеспеченности: Рэmin=1/n, которой соответствует Kmax, и Рэmin=n/n, которой соответствует Kmin.
Эмпирическую кривую обеспеченности строим по данным столбца Pэмп точками и пунктиром интерполируем на глаз.
Дисперсия D характеризует меру рассеяния случайной величины относительно ее математического ожидания.
D = 
= 5185,2224
Среднеквадратическое отклонение:
72,01
После того как построили эмпирическую кривую обеспеченности, строим аналитическую кривую, для того чтобы определить соответствующий модульный коэффициент, а по нему – интересующую нас расчетную гидрологическую характеристику. Гидрологическим явлением отвечают, как правило, асимметричные кривые распределения плотностей вероятности, поэтому аналитические кривые обеспеченности для них будут определяться следующими параметрами: коэффициентами вариации Сv и асимметрии Сs. Т. к. кол-во n-ограничено, то смещённые (неточные) оценки параметров находятся из формул:
Cv =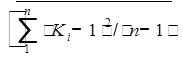 
- коэффициент вариации, Cv =0,513
Cs=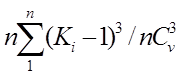
- коэффициент асимметрии. Cs=0,335
Точность этих коэффициентов зависит от количества наблюдений. При таких значениях n как 25 существует большая ошибка вычислений. Для того чтобы её учесть, вычисляют среднеквадратическую ошибку.
;
;
ε Сv = 16%
εСs = 52%
Таким образом в нашей работе коэффициенты Cv и Cs могут отклоняться на величину их относительных ошиболк (±ε). Эта ошибка может быть достаточно большой. Берём учебное пособие Н.Д.Канарский, М.А.Михалёв «Гидрологические расчёты», открываем Приложение 2 – Ординаты кривых трёхпараметрического гамма-распределения. В зависимости от отношения Cs к Cv и значения Cv выбираем параметры распределения.
Допускаем, что Сs/Cv=0,65 и так как в данной таблице есть только отношения равные 0,6 и 0,7 ,то методом интерполяции ((5,28-5,05)/2 +5,05) находим значения Ф. с помощью полученных значений Ф находим К. По данным приложения 2 вышеуказанного пособия строим математическую кривую обеспеченности.
С увеличением коэффициента Сv кривая поворачивается по часовой стрелке .
Существует несколько способов определения несмещенных параметров:
1. Метод моментов
Позволяет корректировать оценки. Определение параметров искомых кривых приводится по случайным выборкам , соответственно сами параметры являются случайными и говорят не о самих параметрах, а об их оценках, которые обладают различной степенью приближения к оцениваемому параметру; чтобы такое приближение было наибольшим:
- чтобы оценка обладала наименьшей возможной дисперсией-такая оценка эффективная.
- должна сходиться к оцениваемому параметру при неограниченном возрастании объема наблюдений- состоятельная;
- должна отсутствовать систематическая ошибка
Для нахождения значения коэффициентов а берём отношение отношение Сs/Cv=0,65,которое ближе всего к значению 2,поэтому выбираем именно строчку с отношением равным двум. Ищем значение r(1)-коэффициент аккориляции (заранее подсчитав значения среднего стока на обеих реках) по формуле и выбираем одну из трёх строк для дальнейших вычислений.
коэффициент аккориляции-степень связи между соседними членами
R(1)=-1565,68/1765,68=-0,09 ( удовлетворяет условиям r(1) <0,5 )
Cv =(а1+a2/n)+(a3+a4/n)*Cv +(a5+a6/n)*Cv =0,52
Cs=(b1+b2/n)+(b3+b4/n)*Cs+(b5+b6/n)*Cs =0,38
2. Метод квантилей
Находим коэффициент скошенности:
S=(Q5%+Q95%-2Q50%)/(Q5%-Q95%)=
Используя биномиальную таблицу считаем среднеквадратичную ошибку:
σ=(Q5%-Q95%)/(k5%-k95%)=
[Q]=Q50%-K50%* σ=
Cv =σ/[Q]=
При оценочных расчетах Cs=Cv
V. Вычисление коэффициента корреляции между максимальными наблюдёнными расходами рек Болва и Ломпадь.
В тех случаях, когда величина относительной среднеквадратичной ошибки нормы изучаемой гидрологической характеристики оказывается больше 10%, продолжительность периода наблюдений считается недостаточной. В этих случаях прибегают к удлинению рядов наблюдений. Основным способом удлинения ряда наблюдений гидрологических расчетных характеристик считается метод аналогий. Применение его возможно при наличии совместных рядов наблюдений на изучаемой реке и реке - аналоге, на которой продолжительность периода наблюдений должно быть достаточна.
Выбор реки-аналога осуществляется в соответствии со следующими факторами:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.