Физика \ Антенны и устройство СВЧ

Цель курсовой работы, ее тематика, содержание и объем пояснительной записки и чертежей, страница 8

Если пренебречь положительной добавкой второго порядка малости,получим

 .

Как и ранее, формулы для ДН определяются видом АР и записываются на оснований соотношений (6) и (7).

Последний пример - симметричное крестообразное затенений круглого раскрыва полосами, параллельными осям OX и OY с шириной

tx и ty соответственно (рио.5).

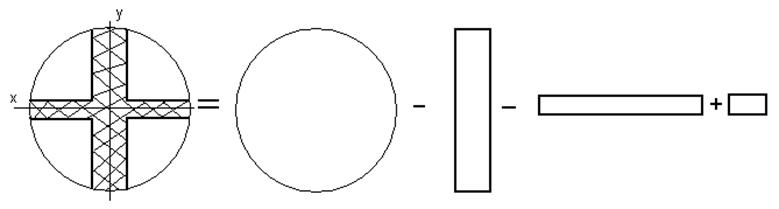
Рио.5. Симметричнее крестообразное затенение круглого раскрыва

Результирующее АР представляется следующей суперпозицией

 , где приняты обозначения составляющих АР:

 - на всем раскрыве;

* - на полосе тени, параллельной оси ОХ;

* - на полосе тени, параллельной оси ОУ;

- на прямоугольнике, образованном пересечением полос.

Приведем выражение для ДН в плоскости XOZ, записанное по формуле (7) с использованием таблицы (с. 15):

 


Следует обратить внимание, что первая ДН относится к круглому раскрыву, а все последующие - к прямоугольному, о чем говорят знаки о и .  В частности, для равномерного АР (простейший случай)

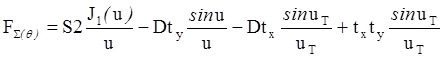 , где      ,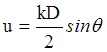

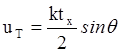
КИП затенения в соответствии с  [19] определяется соотношением

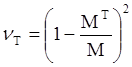 , которое легко позволяет учесть затенение, используя формулы (6), (7),  (9),  (15) и таблицу.

В частности, для последнего примера, где встречаются прямоугольный и круглый раскрывы, для случая равномерного АР

 ;  ;

 .

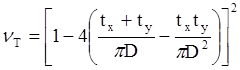Усложним пример, полагая АР в раскрыве в виде "квадратной параболы на пьедестале", и возьмем для определенности   Δ=0,4, a tx=ty=t=0,1D .По формуле (9) с использованием таблицы находим

.

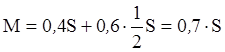На полосе тени АР в одном направлении вдоль большой стороны спадает к краю до 0,4, а вдоль другой t до величины

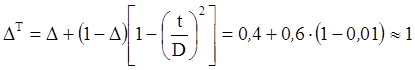 , т.е. практически остается равномерным. Тогда по формулам (15), (9) и таблице находим

 .

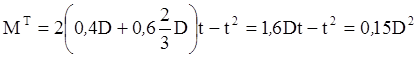Окончательно,

 .

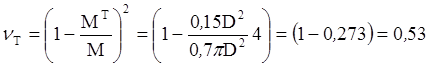9.4. Расчет КИП рассеяния

КИП рассеяния  определяется отношением мощности, попадающей на зеркало антенны, ко всей излучаемой мощности и рассчитывается через ДН облучателя [4]:

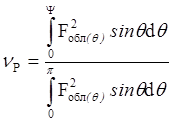  , где Ψ обозначает угол, под которым виден край зеркала из фокуса.

Когда ДН облучателя не является простой функцией или известна в виде графика, полученного ив эксперимента или взятого из литературы, то интегрирование удобно представить графически. Для этого в прямоугольной системе координат на миллиметровой бумаге в пределах до 180° строится нормированная ДН облучателя, возведенная в квадрат. На этом же графике строится функция sinθ. Оба графика перемножаются и составляется отношение площадей под полученной кривой в пределах до θ=Ψ и под всей кривой до θ=180°. Это и будет значение .

9.5. Определение АР в раскрыве зеркала

Распределение возбуждения в раскрыве зеркала зависит от типа зеркала и ДН облучателя. Угловое распределение возбуждения в раскрыве определяется соотношениями [4, 25]:

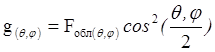
для параболоида вращения и

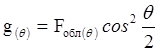
параболического цилиндра.

Чтобы представить АР как функцию координаты плоского раскрыва

(x или y), воспользуемся уравнением параболы

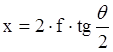 , где f – фокусное расстояние параболы.

Для построения графика АР необходимо, изменяя θ от 0° до значения, под которым виден край зеркала Ψ, вычислить , для тех же углов найти x (y) в, раскрыве и построить АР   g(x) , g(y). Переход от θ к x (у)  может быть проведен и графически.

10.СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

I. Сазонов Д. М., Гридин А . Н . , Мишустин Б. А: Устройства СВЧ: Учеб. пособив /Под ред. Д.М.Сазонова. - М.: Высш.шк., T.98I. - 295 с.

2.Фельдштейн А. Л., Явич Л. Р., Смирнов В. П. Справочник по элементам волноводной техники. - М.: Сов.радио, 1967. - 652 с.

3. Справочник по элементам полосковой техники /Под ред. А.Л.Фельдштейна. - М.: Связь, 1979. - 336 с.

4. Марков     Г. Т., Сазонов    Д . М . Антенны.-М.: Энергия, 1975. - 528 с.

5.Айзенберг Г.З., Ямпольский В. Г. Терешин О.Н. Антенны УКВ. T.I. - М.: Связь, 1977. - 382 с.

6. Драбкин А. Л. , Зузенко В.Л. Кислов А.Г Антенно-фидерные устройства. Сов.радио, 1974. - 506 с.

7. Жук М.Е. Молочков Ю.Б. Проектирование линзовых сканирующих, широкодиапазонных антенн и фидерных устройств. - М.: Энергия, 1973. - 440 с.    

Скачать файл