В тех случаях, когда раскрыв является
плоским, форма прямоугольной или круглой, а распределение фаз одинаковым ![]() выражение для интеграла может быть
максимально упрощено и для не которых видов АР представлено в виде относительно простых функций.
выражение для интеграла может быть
максимально упрощено и для не которых видов АР представлено в виде относительно простых функций.
Обычно сведения о таких АР, формах раскрывов и соответствующих им ДН даются в литературе в виде таблиц [4, с.223; 5,с.152] и т.д. Наиболее употребительны на практике АР вида "спадающее к краю на пьедестале" (рис.1).
![]()
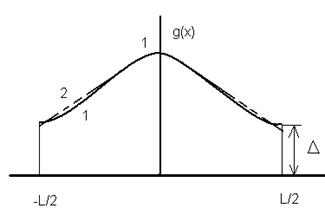
Рис.1. АР вида “спадающее к краю на пьедестале” (1) и его аппроксимация (2)
В упомянутых
таблицах у некоторых АР имеется параметр - величина пьедестала ![]() .
.
При расчетах ДН в этом случае
поступают так: для известного АР в раскрыве (измеренного или рассчитанного)
подбирают аппроксимирующую функцию g1(x) и величину
пьедестала ![]() таким образом, чтобы реальное АР и
аппроксимация его отличались мало. В качестве критерия совпадения разумно
принять совпадение площадей под кривыми при условии незначительного отличия
самих кривых.
таким образом, чтобы реальное АР и
аппроксимация его отличались мало. В качестве критерия совпадения разумно
принять совпадение площадей под кривыми при условии незначительного отличия
самих кривых.
Однако в существующих таблицах набор вариантов аппроксимаций невелик.
Его можно значительно расширить,
применяя теорему о ДН антенн с составными АР [19], которая утверждает:
"Если нормированное АР (![]() )
представляется в виде линейной комбинации нормированных парциальных АР (
)
представляется в виде линейной комбинации нормированных парциальных АР (![]() ) со своими весами (
) со своими весами (![]() )
)
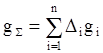 ,
(6) то ДН является линейной
комбинацией соответствующих парциальных ДН (Fi) с теми же весами, умноженными на параметр амплитудного
распределения (Mi),
,
(6) то ДН является линейной
комбинацией соответствующих парциальных ДН (Fi) с теми же весами, умноженными на параметр амплитудного
распределения (Mi),
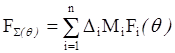 .
(7)
.
(7)
При этом в таблицу должны быть введены параметры амплитудных распределителей, и она примет вид таблицы (с. 16-17).
Формула (6) позволяет при подборе аппроксимирующего АР выражения использовать любую из табличных функций на произвольном пьедестале. На пьедестал можно поставить и линейную комбинацию парциальных АР. Например, АР, соответствующее 3-й строке таблицы, является выпуклым, а 4-й - вогнутым; комбинируя их с необходимыми весами, можно получить любое промежуточное (рис.2),а затем его поставить на пьедестал.
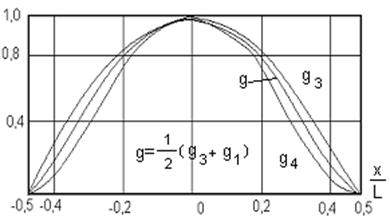
Формула (7) и таблица дают возможность записать выражение для ДН и вычислить ее. При вычислении ДН рекомендуется использовать пакет прикладных программ, описание которых дано в [20]. К соотношениям (6) и (7) нужно добавить правило определения параметра М
для составного АР Рис.2. Пример составного АР
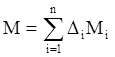 .
(8)
.
(8)
9.2. Апертурный КИП составного АР
Значение КИП апертурной антенны является очень важным, так как сразу позволяет найти ее коэффициент усиления. Полный КИП параболической антенны состоит из нескольких сомножителей
![]() , (9)
, (9)
из которых учтем только три
главных: апертурный (![]() ), КИП рассеяния (
), КИП рассеяния (![]() ) и КИП затенения (
) и КИП затенения (![]() ).
).
Ввиду нелинейной связи между АР и КИП формулы апертурного КИП усложняются и имеют не очень громоздкий вид только для АР, состоящего из двух
![]() ; (10)
; (10)
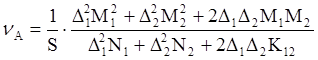 ;
(11)
;
(11)
где Mi и Ni - параметры соответствующих АР из таблицы; S - площадь раскрыва, а 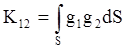 -
интеграл, который нужно вычислять, что усложняет расчеты.
-
интеграл, который нужно вычислять, что усложняет расчеты.
Однако для распространенных АР вида "спадающие к краю на пьедестале ", представленных в форме
![]() , (12)
, (12)
КИП определяется только через табличные параметры М и N
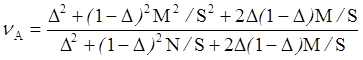 .
(13)
.
(13)
Когда при аппроксимации используется спадающее к краю АР, состоящее из двух (как в формуле (10)), то для нахождения его КИП необходимо вычислять интеграл К12. Но когда этот интеграл вычислен, становится известен параметр N нового распределения
![]() (14)
(14)
(а М определяется просто по формуле (8)) и
имеется возможность подстановки нового АР в формулу (12) и определения ![]() по
соотношению (13).
по
соотношению (13).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.