Изучение элементов волноводных трактов, страница 16

КСВ= 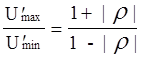 ,  КБВ=  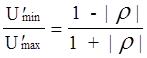.                  ( 3 )   

Откуда

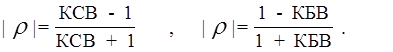                       ( 4 ) 

Рис. 1. Векторные диаграммы и соответствующие им распределения                         напряжения и тока для режимов смешанных (а) и стоячих (б) волн.

Фаза коэффициента отражения находится по сдвигу минимума напряжения относительно конца линии по формуле

, 

как это видно из сравнения диаграмм и распределений , представленных на рис.1.

 2.2. Диаграмма полных проводимостей

При наличии отраженной волны (¹ 0 ) напряжение и ток в ЛП изменяются при перемещении вдоль линии, поэтому изменяется и сопротивление отрезка линии, нагруженного на конце сопротивлением . Значение сопротивления на входе отрезка ЛП  может быть определено из векторной диаграммы напряжений и токов, однако более удобной является специальная  диаграмма полных сопротивлений или проводимостей ( диаграмма Вольперта ), изображенная на рис.2.

Диаграмма строится на плоскости комплексного коэффициента отражения . Линии постоянных значений ôô есть на диаграмме окружности с радиусом, равным ôô. Они имеют общий центр в середине диаграммы. Внешняя окружность диаграммы соответствует ôô= 1, в центре диаграммы   = 0. Линии равных  - радиусы. Обычно линии ôôи   на диаграмму не наносят, а закрепляют в центре вращающуюся линейку с нанесенными на нее значениями  ôô. Значения фазы коэффициента отражения и расстояние, в долях длины волны наносятся по краю внешней окружности диаграммы.

На диаграмму наносятся линии постоянных значений активной  и реактивной составляющих нормированной проводимости  ( или сопротивления  ( ) ).

 Кривые постоянных значений активной проводимости  ( или сопротивления ) представляют собой окружности с центром, расположенным на вертикальной оси диаграммы. Внешней окружности соответствует = 0 . Окружность =1 проходит через центр, при ® ¥  окружность стягивается в точку в нижней части диаграммы. Реактивным проводимостям              (сопротивлениям ) соответствуют дуги окружностей с центрами на горизонтальной прямой касательной к нижней части диаграммы. Вертикальная ось диаграммы ( часть дуги окружности бесконечного радиуса ) соответствует =0, т.е. чисто активным проводимостям, при ® ¥ окружность стягивается в точку в нижней части диаграммы. В правой половине диаграммы реактивности имеют знак  “+ ”, а в левой “ - “(минус).

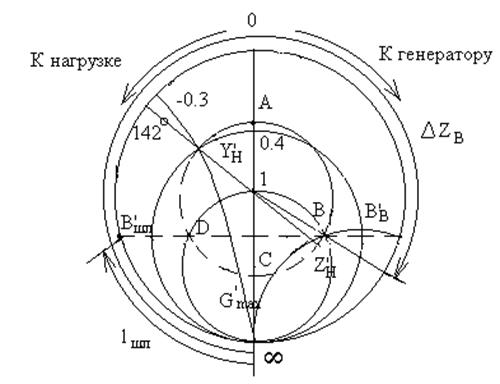
Рис. 2. Диаграмма полных проводимостей

Диаграмма позволяет по известным ôô и    найти  и   (и  ) , для этого линейку поворачивают на угол, соответствующий значению   , и против значения  ôô считывают  и   (и  ) .

И, наоборот, найдя точку пересечения кривых  и   (и  ), поворачивают туда линейку и считывают  ôô и  . На рис.2 показаны кривые, соответствующие нормированной проводимости = 0.4 - j 0.3   . Заметим, что проводимость и сопротивление отражаются на диаграмме диаметрально противоположными точками окружности постоянного ôô.

3.Указания по расчету согласования                         

При экспериментальных измерениях режима работы ЛП определяют положение минимума напряжения Z_min  и  значение КСВ через максимальное и минимальное показания индикатора, затем рассчитывают ôô. В минимуме напряжения, как видно из векторной диаграммы

( рис.1,а ), напряжение и ток совпадают по фазе; следовательно, проводимость является чисто активной и превышает волновую. Этому сечению на диаграмме проводимостей соответствует нижняя точка пересечения вертикальной оси с окружностью измеренного ôô. На рис.2 она обозначена . Если из этой точки в сторону нагрузки по окружности измеренного ôô пройти расстояние DZ_min до конца линии, то можно будет узнать проводимость нагрузки. Расстояние  DZ_min  определяется как разность координат минимумов напряжения в линии с заданной нагрузкой и при коротком замыкании линии на конце

 .                                                   ( 5 )                                         

Для получения согласованного режима (  = 0 ), как видно из формулы ( 2 ), должно выполняться комплексное равенство=1 ( =1 ) , которое разделяется на два вещественных

=1,     =0