Изучение элементов волноводных трактов, страница 15

14.Как провести отсчёт измеренного значения   КСВ ?

15.Опишите процесс измерения коэффициента передачи.

16.Опишите процесс измерения КСВ.

17.Как сосчитать измеренное значение коэффициента передачи ?

ЛИТЕРАТУРА         

1.  Сазонов Д.М.   Антенны и устройства СВЧ: Учебник для радиотехнических специальностей вузов. –М.: Высшая школа, 1988. – 432с.: ил.

Лабораторная работа № 20

Узкополосное согласование

1.Цель работы: исследование режимов работы линии передачи ( ЛП ), измерение сопротивлений нагрузок с использованием измерительной линии, расчет и реализация узкополосного согласования с помощью параллельного шлейфа.

2.Краткие теоретические сведения

     2.1. Режимы работы линии передачи

Напряжение и ток в любом сечении ЛП находятся как наложение двух волн, бегущих в противоположных направлениях. Одна - падающая - движется от генератора к нагрузке, другая - отраженная - движется от нагрузки к генератору. При выборе начала координат на нагрузке и отсутствии потерь в ЛП

,

  , где      - комплексные амплитуды падающих и отраженных волн напряжения и тока, b= 2p/l - коэффициент фазы.

Режим работы ЛП с любой нагрузкой полностью характеризуется коэффициентом отражения,под которым  понимается отношение комплексных амплитуд напряжения отраженной и падающей волн

.

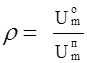С учетом этого нормированные напряжение и ток ( в масштабе падающих волн напряжения и тока ) в произвольном сечении ЛП определяются соотношениями:

,                        

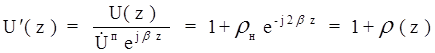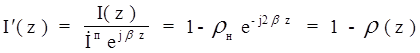,                     ( 1 )                где - коэффициент отражения в сечении нагрузки при Z = 0,

- коэффициент отражения в сечении с произвольной координатой Z.

Знак минус в выражении для тока появляется потому, что  введен как коэффициент отражения по напряжению, а коэффициент отражения по току отличается от него знаком.

На нагрузке ( при Z = 0 ) формулы ( 1 ) дают

, через отношение которых определяется нормированное сопротивление нагрузки

  .   

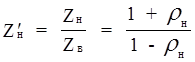Решая относительно  , получаем    

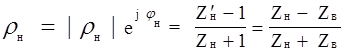.                               ( 2 )                            

По формулам ( 1 ) строится векторная диаграмма напряжений и токов на плоскости комплексного коэффициента отражения, а с помощью векторной диаграммы могут быть получены распределения модулей напряжения  и тока  вдоль линии передачи ( Рис.1).

Перемещению в линии от какого-либо сечения ( Z₁ ) в сторону генератора ( когда координата Z возрастает ) соответствует вращение векторов     _и   - по часовой стрелке, а движению к нагрузке - против часовой стрелке. ( Вектор  -  является коэффициентом отражения по току ). Напряжение на диаграмме представляется вектором, проведенным из начала диаграммы ( точка 0 ) к концу вектора( Z ), а ток - к концу вектора  -( Z ). Длины этих векторов откладываются на графике распределений при соответствующих значениях координаты  Z, которая связана с углом поворота векторов    ( Z ) и -( Z ) от начального положения следующим образом: 

  .       

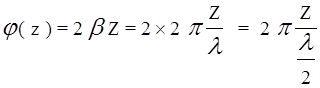Из формулы видно, что векторы совершают полный оборот и графики периодически повторяются, когда Z изменяется на половину длины волны.

Угол Ф между векторами   на рис.1а дает значение фазового сдвига между напряжением и током при данной координате Z.

Вид векторной диаграммы и распределений зависит от значения коэффициента отражения. Когда коэффициент отражения равен нулю напряжение и ток в любом сечении остаются постоянными, сдвиг по фазе между ними отсутствует - такой режим называется согласованным, так как вся энергия от генератора передается нагрузке. В другом крайнем случае, при ôô= 1, напряжения и токи в некоторых сечениях уменьшаются до нуля, а в других, отстоящих на l /4, достигают максимальных значений, вдвое превышающих напряжения и токи падающих волн. Фазовый сдвиг между током и напряжением всюду равен 90⁰, а средняя переносимая мощность равна нулю. Такой режим называется режимом стоячих волн. Распределение напряжения, соответствующее режиму стоячих волн , вызванному коротким замыканием ЛП, представлено рис.1,б.

Степень согласованности режима характеризуется коэффициентами стоячих ( КСВ ) и бегущих ( КБВ ) волн, которые непосредственно находятся по распределению поля