Конструкторская часть. Расчет показателей технологичности. Оценка комплексного показателя качества, страница 5

 

                                                                                                                    f(φ)

 

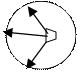
облучатель

     облучатель

                                     Е_s(х)

Отражатель

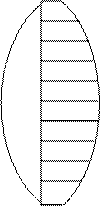
Рисунок 1

Определение геометрических параметров антенны (зеркала), а именно, исходя из заданной величины коэффициента усиления (КУ), определяется площадь излучающего раскрыва и диаметр зеркала.  Далее рассчитывается фокус и длина раскрыва т.к. зеркало предполагается офсетным  (с вынесенным облучателем), то эти расчёты осуществляются для фрагмента на боковой поверхности параболоида вращения, затем, используя требования к диаграмме направленности антенны, определяют размеры рупорного облучателя и его диаграмму в Е и Н плоскостях. По найденным параметрам облучателя и геометрическим параметрам большого зеркала, рассчитывается амплитудное распределение в раскрыве большого зеркала, по амплитудному распределению рассчитывается диаграмма направленности антенны и КУ. Сопоставляя с исходными данными, осуществляется коррекция, например, изменяется (увеличивается или уменьшается) излучающий раскрыв рупорного облучателя, чтобы добиться лучших характеристик зеркала, или увеличивается диаметр зеркала, для уменьшения затенения.

2.3.1 Разработка конструкции антенны (зеркала)

Образующая зеркально-параболических антенн – парабола, есть геометрическое место точек, равноудалённых от точки (фокуса) и от прямой (директрисы). Параболоид вращения – поверхность, образованная вращением параболы вокруг фокальной оси. Длины всех лучей, проведённых из фокуса до параболического зеркала, а затем от зеркала до плоскости раскрыва, постоянны. Отсюда следует, что при облучателе, расположенном в фокусе, поле в плоскости раскрыва параболического зеркала будет синфазно. Это имеет место как для параболоида вращения с точечным облучателем, так и для параболического цилиндра с линейным синфазным облучателем [4].

Основные формулы, связывающие параметры параболоидов вращения:

Уравнение параболы в декартовых координатах имеет вид:

,                                            (1)

где F – фокусное расстояние параболы. В полярных координатах уравнение параболы будет:

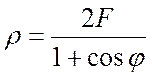                                               ,                                              (2)                 где ρ – радиус-вектор, проведённый из фокуса;

φ – угловая координата (угол между осью ОХ и радиус-вектором).

Угол раскрыва φ (рисунок 2) связан с радиусом зеркала R_n и фокусным расстоянием f соотношением:

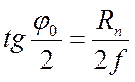;                                         (3)

Из уравнения (2) следует связь между размерами параболического зеркала

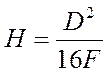                                                     ,                                                     (4)

где Н – высота зеркала, т.е. расстояние от вершины до плоскости раскрыва;

D – диаметр раскрыва для параболоида вращения или ширина раскрыва для параболического цилиндра.

          Угловая апертура зеркала Ф0  связана с фокусным расстоянием F и диаметром зеркала, следующим соотношением, вытекающим из (2) и (4);

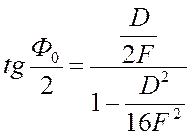                                          .                                         (5)

Коэффициент усиления антенны:

                                            G = η_A * D;                                              (6)

В зеркальных антеннах не вся мощность, излучаемая облучателем, участвует в формировании главного лепестка диаграммы направленности. Часть энергии походит мимо поверхности отражателя. Если мощность, излучаемую облучателем обозначить через Р_обл, а часть мощности, попадающую на поверхность зеркала,  - через Р_з, то, пренебрегая потерями в облучателе и на поверхности зеркала, можно записать:

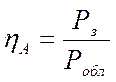;                                        (7)

Коэффициент направленного действия зеркальной антенны зависти от коэффициента использования площади раскрыва ν  и может быть определён из соотношения: