Допуски устанавливают границы, в которых должны находиться параметры. Их подразделяют на производственные, лабораторные, эксплуатационные. Производственные допуски ограничивают погрешности, возникающие при производстве. Лабораторные допуски ограничивают производственные погрешности и отклонения, возникающие при исправлениях (лабораторный допуск должен быть шире производственного). Эксплуатационные допуски ограничивают погрешности, возникающие при эксплуатации (испытание на повышенных температурах).
Допуски подразделяются на механические и электрические, в зависимости от погрешностей параметров, которые они ограничивают.
Предельные
значения параметров ![]() :
:
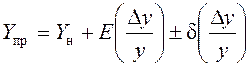 , (6.1) где
, (6.1) где
![]() – номинальное значение;
– номинальное значение; 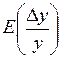 - отклонение середины поля допуска от
номинального значения (координаты середины поля допуска);
- отклонение середины поля допуска от
номинального значения (координаты середины поля допуска);
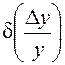 - половина
поля допуска.
- половина
поля допуска.
На использовании уравнения погрешностей основываются методы предельных отклонений и вероятностей.
Метод предельных
отклонений.Если использовать уравнение погрешностей:
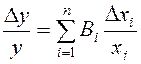 , то можем записать:
, то можем записать:
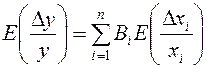
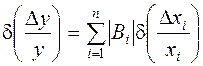 (6.2)
(6.2)
(6.3)
Эти выражения и являются основными при подборе допусков методом
предельных отклонений.
Вероятностный метод расчета электрических допусков
Необходимо
определить 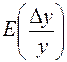 и
и 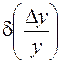 .
.
Начнем с решения первой задачи. Используя уравнения погрешностей и применяя правило сложения математических ожиданий, запишем:
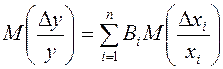 . (6.4)
. (6.4)
Связь между математическим ожиданием и отклонением ![]() устанавливается известным уравнением
Бородачева.
устанавливается известным уравнением
Бородачева.
Так как радиоэлементы
изготавливаются в крупносерийном и массовом производстве, то их погрешности
подчиняются, как правило, нормальному закону
распределения. В этом случае коэффициенты относительной асимметрии равны нулю:
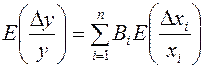
Как видно, это уравнение полностью совпадает с методом предельных отклонений.
Выражение
для половины поля допуска 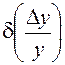 выходного параметра.
выходного параметра.
Используют
относительное рассеивание: 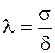 , (6.6)
, (6.6)
где ![]() - среднеквадратичное отклонение
погрешности;
- среднеквадратичное отклонение
погрешности; ![]() - половина поля допуска.
- половина поля допуска.
Получаем: 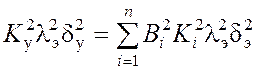 , где
, где
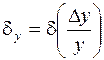 ;
; 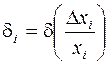 , или
, или
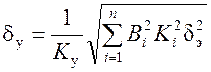 , где
, где ![]() - коэффициент влияния;
- коэффициент влияния; ![]() - коэффициент относительного рассеивания;
- коэффициент относительного рассеивания;![]() - коэффициент относительного рассеивания
выходного параметра.
- коэффициент относительного рассеивания
выходного параметра.
Если
законы распределения первичных параметров нормальные, то коэффициенты
относительного рассеивания ![]() и
и ![]() равны единице.
равны единице.
Произведём расчёт необходимых размерных цепей для данной дипломной работы:
При анализе разрабатываемой конструкции можно сделать вывод, что наибольшие трудности могут возникнуть при сборке системы крепления и ориентации зеркала, в особенности при совмещении кронштейнов АБВГ.745535.001 и АБВГ.745313.001 (см. сборочный чертёж АБВГ.315231.001 СБ). Также поведём расчёт для общей сборки (см. АБВГ.301560.001 СБ), точнее для соединения системы крепления и ориентации с зеркалом. Расчёт будем проводить методом предельных отклонений и вероятностным: проведём расчёт для кронштейна АБВГ.745535.001:
ai = aj = 0,15;
Кi = Кj = 1,3.
A1 = 120 - 0,87
A2 = 30 – 0,21
А3 = 30 – 0,21
Составим размерную цепь:
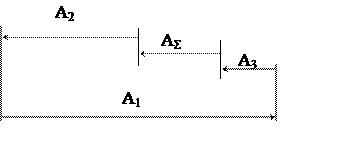 |
А1 — увеличивающее звено E1= – 0,435 d1= 0,435
А2 — уменьшающее звено E2= – 0,105 d2= 0,105
А3 — уменьшающее звено E3= – 0,105 d3= 0,105
АΣ — замыкающее звено
Метод предельных отклонений.
— Номинальный размер замыкающего звена:
![]()
— Середина поля допуска:
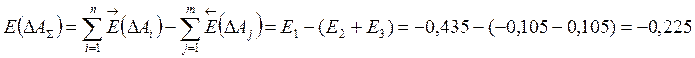
— Половина поля допуска:
![]()
— Расчёт предельных размеров замыкающего звена:
![]()
Вероятностный метод.
— Коэффициент относительной асимметрии:
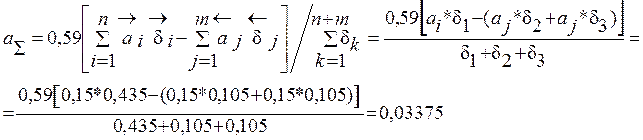
— Коэффициент относительного рассеивания:
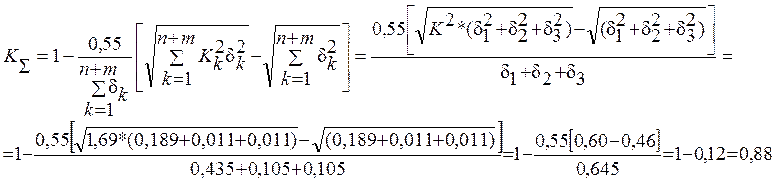
— Половина поля допуска:
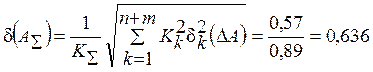 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.