Преобразование подобия плоскости. Гомотетия и её свойства

11. Преобраз-ие подобия пл-ти. Гомотетия и её св-ва. Опр: Преобраз-ием под-я наз-ся такое преобраз-ие пл-ти, при кот-ом все расст-я изменяются в одинаковое число раз (это число наз-ся коэфф-ом под-я, k и k>0). под-е с коэфф-ом k;  тогда k*AB = A’B’. Если k=1, то расст-я не изменятся  D – частный случай  Опр: 2 фигуры наз-ся подобными, если одну из них в другую можно перевести с помощью преобраз-ия под-я.  F1 подобно F2  (F1 M-эквивалентно F2); (F1 конгруэнтно F2, т.е.такое D-ие, кот-ое переводит F1 в F2). Для подобия фигур имеют место рефлекс-ть, транзит-ть, симметрич-ть - это след-ет из Th о G – эквивалентности. Св-ва преобраз-ия под-я: 1. Преобраз-ие под-я, отличное от D-ия не может иметь более одной неподвиж-й (.)-и. Док-во(от прот-ого): причём AB=1*AB, k=1 ?! (если (.)-и перешли в себя, то расст-ие м/д ними осталось тем же). 2. При преобраз-ии под-я: а) окруж.окруж.; б) отрезокотр.,  прямаяпрямую, луч луч; в) ||-ые прямыев ||-ые прямые. Док-во: б) отрезокотр. Пусть ]AB[ = {M: AM+MB=AB}*. Пусть  Пусть  тогда A’M’=k*AM, M’B’=k*MB, A’B’=k*AB; т.к. для М выпол-ось рав-во *, домножим на k, получим: k*AM+k*MB=k*AB A’M’+M’B’=A’B’ (по опр-ию). Т.о. т.к. М – произв-ая M(]AB[)]A’B’[. Аналог-о, рассмотрев преобраз-ие  покажем обратное включение, а именно: M(]AB[) ]A’B’[. Из (1) и (2)  M(]AB[)=]A’B’[, т.к.  M([AB])=[A’B’]. Ч.Т.Д.

3. При преобраз-ии под-я сохран-ся отнош-е любых отрезков. 4. При преобраз-ии под-я угол переходит в равный ему угол. Док-во:

угол угол (это следует из того, что лучлуч). Т.д. . Док-во: A и B – произв-ые на h и m; Пусть  Рассмотрим и 

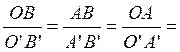
(т.к. это преобраз-ие под-я); из школы известно, что соответственные углы в этих - х равны, т.е. . Ч.Т.Д.

5. При преобраз-ии под-я все площади измен-ся в раз. Th: Мн-во всех под-ий пл-сти образует группу. Док-во: 1. Пусть  преобраз-ия под-я. Пусть A, B – произвольные точки;   Т.к. под-е, то  Т.к. под-е, то     Т.к. под действием композиции произв-ый отрезок AB изменился в раз, то эта композиция есть под-е с коэфф-ом  2. Пусть A’ и B’ – произвольные, а A и B их прообразы;  A’B’ = k*AB (*);   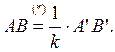 Под действием преобраз-ия произв-ый отрезок A’B’ изменился в одну k-ую раз, т.е. (преобраз-ие под-я).Гомотетия. Опр: гомотетией с центром в (.)-е О и коэфф-ом наз-ся такое преобраз-ие пл-ти, при кот-м (.)-а О остаётся на месте, а произв-ая (.)-а А переходит в такую (.)-у , что  Пр-р: 1)        

2)                                             

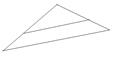
Св-ва: 1. Еслиотображаетто

Следствие из св-ва 1(Th-а): Гомот-я с коэфф-ом k есть преобраз-ие под-я с коэфф-ом |k|. Док-во: Это следует из доказанного рав-ваи опр-ия умножения век-ра на число.

(опр-ие * век-ра на число) A’B’ = k*AB. Ч.Т.Д., т.е. все св-ва подобия вып-ся. 2. При гомот-ии прямые, проходящие ч/з центр переходят в себя, не проходящие ч/з центр переходят в ||-ые себе прямые. 3. Гомот-я не меняет ориентацию пл-сти. 4. Любые две неравные окружности дважды гомотетичны (Если 2 окр-ти имеют разные R-сы, то одну в другую можно отобразить двумя гомотетиями). Уравн-ие гомот-ии. P(a, b) и коэфф-т  

P(a, b)                                        A'(x’, y’)

Пусть A(x, y) – произв-ая точка;  

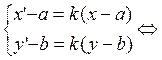
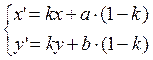Ур-ие гомот-ии.

Частный случай. Если центр гомот-ии O(0; 0), то 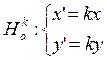Ур-ие гомот-ии с центром в начале коорд-т. Th: Любое преобраз-е под-я можно разложить в композицию гомот-ии с произв-ым центром и D-я. Док-во: Пусть произв-ое преобраз-ие под-я. Рассмотрим   (* насправа);  (P–произв. центр);  

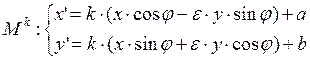 Ур-ние подобия.