Числовая последовательность. Основные понятия дисциплины

12. Числовая последовательность

Начнем с установления понятия числовой последовательности. Представим себе натуральный ряд:1,2,3,…,n,…n’,…  (1)

В котором числа расположены в порядке возрастания, так что большее число n’ следует за меньшим nЕсли теперь заменить в ряде (1) по какому – нибудь закону каждое натуральное число n на вещественным числом x_n, то получится числовая последовательность x₁,x₂,x₃,…,x_n,…,x_n’  (2)

Будем называть члены последовательность их номерами.

Числовую последовательность будем отмечать точками на числовой оси.

Т.к. числовая последовательность есть функция числового аргумента, то для нее применимы все свойства и определения, которые свойственны для функции(ограниченность, монотонность, и т.д.)

Числовая последовательность называется строго возрастающей, если

Числовая последовательность называется строго убывающей, если

Введем такое понятие как понятие окрестности точки a, где

Пусть - произвольная;, тогда - окрестностью называется интервал ()

Действительное число а называется пределом числовой последовательности x_n при (), если найдется такой номер , что для всякого выполняется неравенство , при этом пишут так:

Рассмотрим геометрический смысл данного определения

Если , есть радиус - окрестности точки a, при все члены последовательности начиная с некоторого номера  попадают в - окрестности точки a. 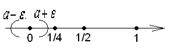Для любой окрестности точки a найдется такой номер, начиная с этого номера се члены последовательности попадут в эту - окрестность. Чем меньше , тем больше должно быть номер . . 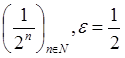Все элементы без Х₁ - - окрестность.

Пусть =1/4,  =

Пусть =1/16,  =

Начиная с 5-ого элемента (х₅) все члены последовательности будут находиться в- окрестность радиусом 1/16.

Всякая числовая последовательность имеющая своим пределом число , назыв сходящейся

     - сходящаяся к «0»

Свойства:

1.  Теорема: Если последовательность  имеет предел и он равен а, и а>р, то  начиная с которого

 и а>р 

По условию а>póa-p>0 в качестве  возьмем число равное а-р и рассмотрим определение пределов

=а-р; ; => x_n>p

Начиная с все номера больше р.

2.  Т: если   и а<q 

=q-a>0; ; x_n<q

3.  Т: если последовательность имеет предел, то он единственный.

 - единств

Пусть существует еще один предел числовой последовательности

 и ,ab, a<b, a<r<b, r=(b-a)/2

1)  a<r  по 2⁰                                          противоречие

2)  b>r  по 1⁰                                        

4.  Т: Если числовая последовательность имеет предел, то она ограничена.

Рассмотрим произвольную - окрестность. Содержит все члены последовательности за исключением некоторого конечного их числа

Пусть ,

Т.к. множество значений числовой последовательности ограничено и сверху и снизу, то числовая последовательность является ограниченной. Обратное говоря неверно.

Теореме Вейштрасса: 1. Если возрастает или строго возрастает числовая последовательность ограниченная сверху, то она имеет конечный предел, в противном случае

2.  Если убывает или строго убывает числовая последовательность ограниченная снизу, то она имеет конечный предел, в противном случае

Докажем 1.: Пусть - возрастает; - огр сверху

Множество значений - ограничено

 ;

1)  - верхняя граница;

2)  - наименьшая верхняя граница;

Из этих 2-х условий следует, что если мы построили на  - окрестность, то на основании 2-ого будем иметь следующее, ,

Из того, что последовательность возрастающая =>

Т.о. ()ó

Допустим теперь, что таже последовательность - не огр сверху, - больше любого сколь угодно большого наперед указанного числа.

, т.к. последовательность возрастает поэтому, начиная с некоторого номера все члены последовательности будут иметь положительный знак.

Докажем 2.: Пусть - убывает; - огр снизу, поэтому

 =;Покажем, что

1) 

2) 

Рассмотрим произвольную - окрестность точки .

(;

(;

Допустим теперь, что таже последовательность - не огр снизу, - больше любого сколь угодно большого наперед указанного числа.

С числ.посл-ми уч/ся встр-ся в курсе 9 кл. опр ч.п. не дается. Числовая посл-сть может быть  задана формулой n-го члена, рекурентной форм-й. Рассм-ся 2 вида посл-й: арифм и геом-я прогр-и. После введ-я опр ариф пос-ти, затем жел-но методом  мат инд-и привести уч/ся к формуле n-го члена арифм прог-и. При реализации контроля при изучении числовой последовательности