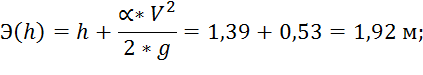
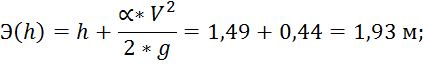
4. Разность значений удельной энергии:
![]()
5. Средняя глубина на участке:
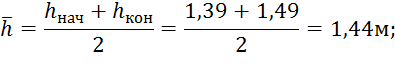
6. Новая площадь живого сечения на участке:
![]()
7. Смоченный периметр:
![]()
8. Гидравлический радиус:
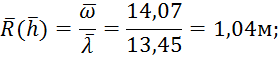
9. Коэффициент Шези:
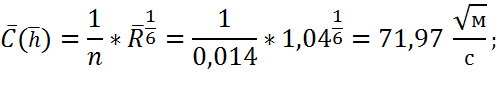
10.Уклон дна на данном участке:
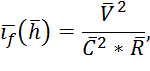
где скорость на участке высчитывается по формуле:
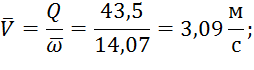
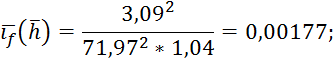
11.Разность уклонов:
![]()
12.Разность продольных координат сечения:
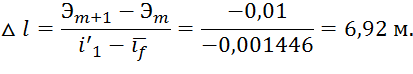
По полученным точкам строим кривую спада на отводящем участке канала (рис. 8).
3. Расчет гидравлического прыжка
Гидравлическим прыжком называется
явление резкого увеличения глубины от ![]() до
до ![]() , при котором поток из бурного
состояния переходит в спокойное. Глубины h’ и
h’’ называются сопряженными, h’ – первой, а h’’
– второй сопряженной глубиной. При этом явлении энергия вдоль потока
уменьшается.
, при котором поток из бурного
состояния переходит в спокойное. Глубины h’ и
h’’ называются сопряженными, h’ – первой, а h’’
– второй сопряженной глубиной. При этом явлении энергия вдоль потока
уменьшается.
3.1.Построение графика прыжковой функции ![]()
Для построения графика будем использовать уравнение гидравлического прыжка, которое устанавливает связь между сопряженными глубинами:
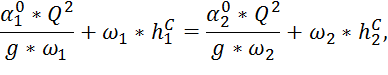
где ![]() – коррективы кинетической энергии и
равны 1,
– коррективы кинетической энергии и
равны 1, ![]() – ускорение свободного падения,
– ускорение свободного падения, ![]() –
расход воды в канале,
–
расход воды в канале, ![]() – площадь живого сечения, а
– площадь живого сечения, а ![]() – заглубления центра тяжести.
– заглубления центра тяжести.
При заданных расходе Qи форме поперечного сечения русла
(в нашем случае трапецеидальная форма поперечного сечения) выражения в правой и
левой частях уравнения зависят только от глубины h, что делает целесообразным обозначить эти выражения
через ![]() :
:
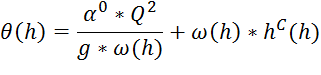
и называть ![]() прыжковой функцией. При этом
уравнения гидравлического прыжка можно записать в виде:
прыжковой функцией. При этом
уравнения гидравлического прыжка можно записать в виде:
![]()
График прыжковой функции строится по тому же принципу, что и график удельной энергии сечения, по точкам. Для удобства значения расчетов сведем в таблицу.
|
№ |
|
|
|
|
|
|
м |
|
м |
|
|
|
|
1 |
0,50 |
3,90 |
0,239 |
49,51 |
50,44 |
|
2 |
0,60 |
4,80 |
0,284 |
40,17 |
41,54 |
|
3 |
0,80 |
6,74 |
0,373 |
28,63 |
31,15 |
|
4 |
1,00 |
8,85 |
0,460 |
21,82 |
25,89 |
|
5 |
1,15 |
10,54 |
0,524 |
18,32 |
23,85 |
|
6 |
1,20 |
11,12 |
0,545 |
17,36 |
23,43 |
|
7 |
1,30 |
12,32 |
0,587 |
15,67 |
22,91 |
|
8 |
1,39 |
13,44 |
0,625 |
14,36 |
22,76 |
|
9 |
1,50 |
14,85 |
0,670 |
13,00 |
22,96 |
|
10 |
1,60 |
16,17 |
0,711 |
11,93 |
23,44 |
|
11 |
1,70 |
17,54 |
0,752 |
11,00 |
24,19 |
|
12 |
1,90 |
20,41 |
0,832 |
9,46 |
26,45 |
|
13 |
2,50 |
30,00 |
1,067 |
6,43 |
38,47 |
|
14 |
3,00 |
39,15 |
1,258 |
4,93 |
54,20 |
Пример расчета таблицы для h=1м:
1. Площадь живого сечения:
![]()
2. Глубина центра тяжести:
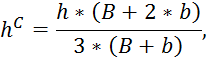
где B – ширина сечения канала по верху, равная:
![]()
Соответственно, глубина центра тяжести:
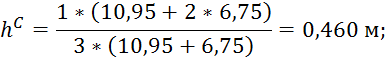
3.
Значение ![]() :
:
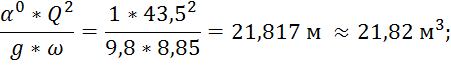
4. Значение прыжковой функции:
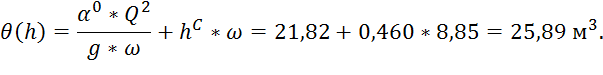
По полученным точкам строим график прыжковой функции и совмещаем ее с графиком удельной энергии (рис. 9).
3.2.Построение линии сопряженных глубин для кривой типа ![]() и определение местоположения прыжка
и определение местоположения прыжка
Нам необходимо построить линию сопряженных глубин для вторых сопряженных глубин h’’. Для этого составим таблицу.
|
h’, м |
0,34 |
0,55 |
0,76 |
0,97 |
1,18 |
1,39 |
|
h’’, м |
3,20 |
2,80 |
2,2 |
1,90 |
1,65 |
1,39 |
В этой таблице h’ – первые сопряженные глубины,
значение которых соответствуют значениям глубин для кривой подпора типа ![]() на отводящем участке, а h’’ – вторые сопряженные глубины. Зная значения
первых сопряженных глубин, можем найти соответствующие им значения вторых
глубин по графику прыжковой функции. Для этого используем уравнение
гидравлического прыжка в следующем виде:
на отводящем участке, а h’’ – вторые сопряженные глубины. Зная значения
первых сопряженных глубин, можем найти соответствующие им значения вторых
глубин по графику прыжковой функции. Для этого используем уравнение
гидравлического прыжка в следующем виде:
![]()
Теперь построим линию сопряженных
глубин (рис. 8). Точка пересечения линии сопряженных глубин с линией спада типа
![]() соответствует концу прыжка, т.е. это
вторая действительная сопряженная глубина, равная 1,85 м. Соответственно,
обратным ходом по графику прыжковой функции найдем действительное значение
первой сопряженной глубины. Таким образом, получаем:
соответствует концу прыжка, т.е. это
вторая действительная сопряженная глубина, равная 1,85 м. Соответственно,
обратным ходом по графику прыжковой функции найдем действительное значение
первой сопряженной глубины. Таким образом, получаем:
![]()
![]()
Отметим первую действительную сопряженную глубину на
кривой подпора типа ![]() . Соединив две сопряженные глубины,
получаем гидравлический прыжок. Красным цветом покажем реальные получившиеся
кривые свободной поверхности на отводящем участке канала (рис. 8).
. Соединив две сопряженные глубины,
получаем гидравлический прыжок. Красным цветом покажем реальные получившиеся
кривые свободной поверхности на отводящем участке канала (рис. 8).
3.3.Определение длины гидравлического прыжка и потери энергии в нем
Высота гидравлического прыжка высчитывается как разность сопряженных глубин:
![]()
Для определения длины гидравлического прыжка имеется эмпирическая зависимость:
![]()
Потеря энергии в пряжке находится по формуле:
![]()
Рассмотрим уменьшаемое и вычитаемое отдельно.
1. Удельная энергия, соответствующая первой сопряженной глубине:
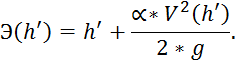
Чтобы найти скорость, сначала необходимо найти площадь живого сечения:
![]()
Таким образом, скорость равна:
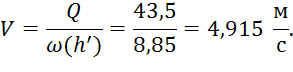
Теперь можем найти значение удельной энергии сечения:
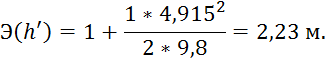
2. Удельная энергия, соответствующая второй сопряженной глубине:
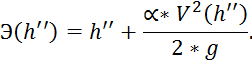
Чтобы найти скорость, сначала необходимо найти площадь живого сечения:
![]()
Таким образом, скорость равна:
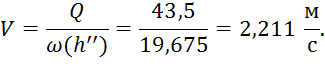
Теперь можем найти значение удельной энергии сечения:
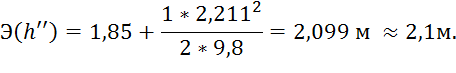
Потеря энергии в прыжке:
![]()
Схема гидравлического прыжка с нанесением напорной линии представлена на рис. 10.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.