Расчет канала на равномерное и неравномерное движение. Расчет гидравлического прыжка, страница 2

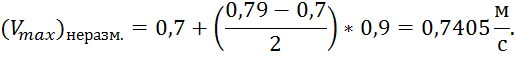
Чтобы найти максимально допустимую скорость на отводящем участке для диаметра 1,5 мм, надо интерполировать полученные значения:

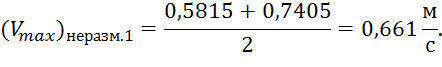
Аналогично делаем и для отводящего участка с нормальной глубиной 2,2 м.

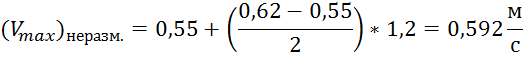
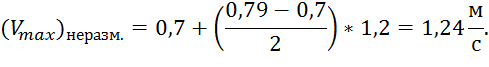
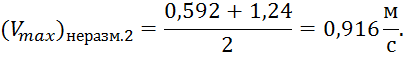
Чтобы участки не размывались, должны выполняться условия:

Сравнив, получаем, что на подводящем и отводящем участках скорости больше максимально допустимых значений. Следовательно, участки будут размываться.

1.4.Определение глубины наполнения и уклона дна канала, полагая

На подводящем участке не допустим размыв дна. Поэтому примем скорость на этом участке равной максимально допустимой -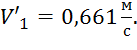

Зная скорость, необходимо найти новую нормальную глубину и уклон дна подводящего участка.

Найдем новую площадь живого сечения:

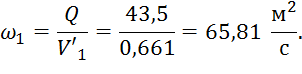
В то же время площадь живого сечения можно найти по формуле:

Соответственно, приравнивая эти два выражения, получаем квадратное уравнение, из которого можно найти новую нормальную глубину:

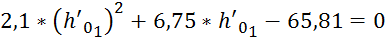
Для того, чтобы найти уклон, воспользуемся преобразованной формулой Шези для скорости:

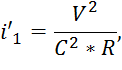
где R (гидравлический радиус) находится по формуле:

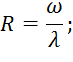
В свою очередь смоченный периметр находится по формуле:

,

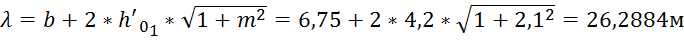а новая площадь живого сечения:

Таким образом, получаем:

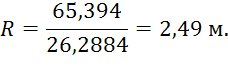
Зная гидравлический радиус, можно найти коэффициент Шези:

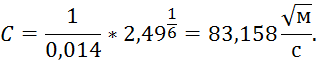
Теперь можем рассчитать уклон:

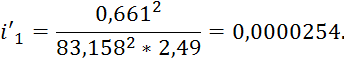
Таким образом, получаем новые значения:

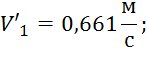
2.  Расчет канала на неравномерное движение

2.1.Определение критической глубины и критического уклона

Частное значение полного (гидродинамического) напора, вычисленное в предположении, что плоскость сравнения проходит через самую нижнюю точку живого сечения, называется удельной энергией сечения и обозначается Э.  Так как функция Э(h) непрерывна, то всегда существует минимум этой функции.

Глубина, отвечающая минимуму удельной энергии, называется критической и обозначается .

Можно найти уравнения для  из условия, что :

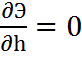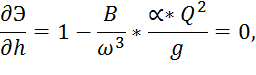
где B – ширина канала по верху,  – площадь живого сечения,  – корректив кинетической энергии (, Q – расход воды в канале, а g – ускорение свободного падения.

Из уравнения получаем:

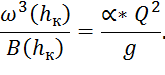
В общем случае это уравнение решается графически.

Для начала найдем значение правой части уравнения:

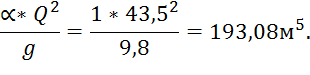
Критическую глубину находим методом подбора. Задаёмся неизвестной величиной и вычисляем все необходимое. Значение глубины выбираем произвольно. Для удобства построим таблицу.

Величина	h	B
Единицы измерения	м	м
Значения величин	1	10,95	8,85	63,30
	1,2	11,79	11,12	116,75
	1,3	12,21	12,32	153,29
	1,4	12,63	13,56	197,67
	1,5	13,05	14,85	250,94

Пример расчета с h=1 м:

1.  Ширина канала по верху:

где b – ширина канала по дну, равная 6,75 м, m- коэффициент откоса канала, равный 2,1. Подставив значения, получаем:

2.  Площадь живого сечения:

где все значения нам известны и, подставив, получаем:

3.  Значение :

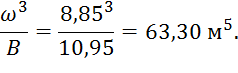
По полученным значениям строим график зависимости глубины от значения .  Значение критической глубины можно найти, отложив на нем уже найденную величину правой части уравнения (рис. 4).

Получаем, что

Критический уклон найдем по формуле:

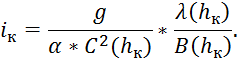
Зная критическую глубину, вычислим все необходимые характеристики канала, чтобы найти критический уклон:

1.  Площадь живого сечения:

2.  Ширина канала по верху:

3.  Смоченный периметр:

4.  Гидравлический радиус:

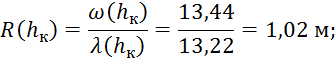
5.  Коэффициент Шези:

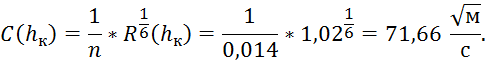
Теперь можем найти критический уклон:

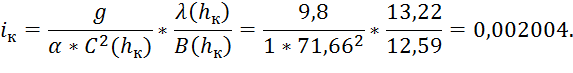
Поперечное сечение канала с критической глубиной представлено на рис. 5.

2.2.Построение графика удельной энергии сечения

Определение удельной энергии было дано в предыдущем пункте (см. п. 2.1). График строится по точкам. Для удобства значения расчетов сведем в таблицу.

м		м/с	м	м
0,60	4,806	9,051	4,179	4,779
0,80	6,744	6,450	2,122	2,922
1,00	8,850	4,915	1,232	2,232
1,15	10,540	4,127	0,869	2,019
1,20	11,124	3,910	0,780	1,980
1,30	12,324	3,529	0,635	1,935
1,39	13,440	3,236	0,534	1,924
1,50	14,850	2,929	0,437	1,937
1,60	16,176	2,689	0,368	1,969
1,70	17,544	2,479	0,313	2,013
1,90	20,406	2,132	0,232	2,132
2,50	30,000	1,450	0,107	2,607
3,00	39,150	1,111	0,063	3,063
4,00	60,600	0,717	0,026	4,026

Пример расчета таблицы для h=0,6 м:

1.  Площадь живого сечения:

2.  Скорость:

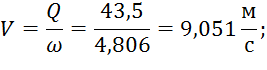
3.  Скоростной напор:

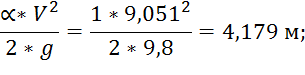
4.  Удельная энергия:

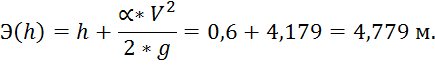
По полученным значениям строим график зависимости удельной энергии сечения от глубины потока. Биссектриса первого координатного угла является асимптотой удельной энергии сечения. Отложив критическую глубину на графике, видно, что ей соответствует минимум функции, согласно определению (рис. 6).

2.3.Построение кривой свободной поверхности на подводящем участке канала