Оценка скорости горения горючих смесей при переменных давлениях и температурах, страница 3

Перейдём к выводу условия самоподдерживающейся волны Чепмена-Жуге. Из первых двух уравнений в системе (3),исключив массовую скорость u, получим уравнение прямой Михельсона в плоскости (P, V):

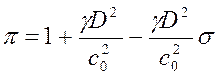                                             ,                                             (5)

Её наклон зависит от скорости волны D. Приравнивая прямую Михельсона к адиабате энерговыделения (4), получим уравнение вида

a(D)s²+b(D)s+c(D)=0,                                               (6)

параметрически зависящее от скорости D. В этом уравнении

,

,

.

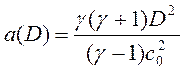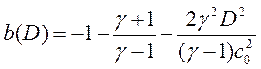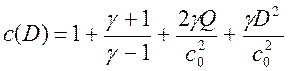Решая уравнение (6) относительно s, получим два корня, также параметрически зависящие от волновой скорости D[2]:

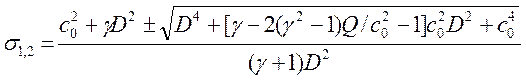                  .                  (7)

При D>c₀ получим секущую и две точки пересечения с детонационной ветвью адиабаты энерговыделения (P>P₀ и V<V₀), при D<c₀ – с ветвью горения адиабаты энерговыделения (P<P₀ и V>V₀) (рис. 1). Две точки пересечения стягиваются в одну тогда и только тогда, когда подкоренное выражение в (7) равно нулю [2]:

                              .                              (8)

Уравнение (8) и есть искомое условие Чепмена-Жуге, которое замыкает систему уравнений (3) и позволяет вычислить все неизвестные параметры за детонационной волной (волной горения) P, r, u.

Решение уравнения (8) даёт: касательную 3 с точкой касания Dна рис. 1 и скоростью самоподдерживающейся волны детонации Чепмена-Жуге ±D_DO, а также касательную 4 с точкой касания Fи скоростью самоподдерживающейся волны горения Чепмена-Жуге ±D_FO(рис. 1). Отметим, что уравнение (8) является биквадратным уравнением относительно скорости D, то есть для него справедлива формула Виета, согласно которой произведение корней уравнения равно свободному члену:

, или [2, 4]:

                                                                                                  (9)

Соотношение (9) является определяющим соотношением между самоподдерживающимися скоростями горения и детонации в рамках предложенной модели, с помощью которого можно получить зависимость скорости горения от давления и температуры.

1.2.  Взгляд на горение со стороны детонации и зависимость скорости горения от давления и температуры.

Рассмотрим детонационную волну относительно точки исходного состояния О (см. рис. 1). Ударная волна переводит газ из состояния О в состояние S, соответствующее химпику детонационной волны, затем начинается химическая реакция и после ее завершения продукты реакции попадают в точку D. Переход из S в D осуществляется вдоль прямой Михельсона, являющейся касательной к адиабате энерговыделения относительно исходного состояния О. Но прямая Михельсона из О в S одновременно является касательной к адиабате энерговыделения, проведенной из точки S как начальной [4]. Следует уточнить, что адиабаты энерговыделения, построенные относительно точек О и S, не совпадают друг с другом, сохраняется лишь условие и точка касания D. При этом изоэнтропа в точке D касается снизу адиабаты энерговыделения, построенной относительно точки О, и касается сверху адиабаты, построенной относительно точки S. Иными словами, точка D соответствует как параметрам детонации относительно исходного состояния О, так и - параметрам горения с исходным состоянием в точке S. Этот взгляд (со стороны детонации на горение) позволяет проанализировать изменение скоростей горения в состояниях с различными начальными давлениями и температурами и получить [5] аналитическую формулу для скорости горения в зависимости от Р₀ и Т₀ .