Оценка скорости горения горючих смесей при переменных давлениях и температурах, страница 2

Следует отметить, что в величинах экспериментальных значений скоростей пламени существует заметный разброс, обусловленный не только различными методиками определения нормальной скорости пламени (горелка Бунзена, распространение пламени в вертикальной трубе вверх или вниз, расширение сферического пламени в мыльном пузыре или бомбе постоянного объема, горение во встречных потоках горючего и окислителя и т.д.). Часто скорость нормального пламени D пересчитывается через видимую скорость пламени D_* с помощью соотношения

                                                     ,                                                     (2)

где s - степень расширения продуктов сгорания [1].

С другой стороны, к задаче о зависимости скорости горения D от давления и температуры можно  подойти с точки зрения детонационных процессов.

1.1.  Классическая теория детонации и горения.

Классическая теория детонации и горения хорошо известна и подробно изложена в книгах [2, 3]. Она базируется на законах сохранения массы, импульса и энергии:

,

                                           ,                                           (3)

.

Здесь r - плотность смеси, P - давление, D и u - волновая и массовая скорости, I - энтальпия, Q - энерговыделение смеси (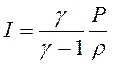 для политропных газов, g - показатель адиабаты). Для простоты математических преобразований в модели сделаем основные допущения: g, отношение теплоёмкости при постоянном давлении к теплоёмкости при постоянном объёме, постоянна и не зависит ни от температуры, ни от состава смеси; Q – постоянна вдоль всего процесса (химическая реакция происходит мгновенно) [4].

Из третьего уравнения в системе (3), исключив неизвестные параметры Dи u при помощи первых двух соотношений, можно получить адиабату продуктов реакции P=f(V,Q) – адиабату энерговыделения, представляющую собой гиперболу в плоскости (P,V), выпуклую в сторону начала координат (V≡1/r –удельный объем смеси):

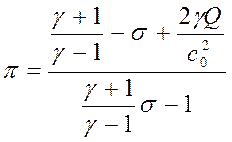                                                    .                                                    (4)

Здесь и далее приняты стандартные обозначения  в газодинамике p=P/P₀, s=V/V₀, 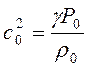 - скорость звука в исходной горючей смеси. На этой гиперболе выделяют детонационную ветвь (при P>P₀ и V<V₀) и ветвь горения (при P<P₀ и V>V₀). Поскольку точка исходного состояния лежит «вне гиперболы», то из этой точки к ветвям горения и детонации адиабаты энерговыделения можно провести прямолинейные секущие с двумя точками пересечения этой прямой с каждой ветвью адиабаты энерговыделения. Эти секущие традиционно называются прямыми Михельсона. Точки пересечения стягиваются в одну, когда секущая превращается в касательную. Условие касания (будет получено ниже) задаёт определённый режим распространения волн горения и детонации, который традиционно называют самоподдерживающейся волной Чепмена-Жуге [2,3,4]. На рис. 1, представляющего собой диаграмму состояний горючей смеси и продуктов, изображена описанная адиабата 1 вместе с ударной адиабатой Гюгонио 2 (химическая реакция не происходит, Q=0).

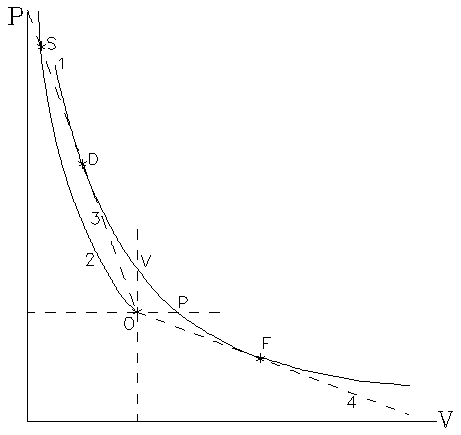
Рис. 1. Типичная диаграмма состояний исходной горючей смеси и продуктов реакции и её особые точки.

На диаграмме есть несколько важных точек (см. рис.1): точка О – начальное состояние; пунктирные прямые 3 и 4 – касательные к ветвям детонации и горения адиабаты энерговыделения, проведенные из точки О; точка D соответствует параметрам детонации Чепмена-Жуге – скорость распространения D_DO; точка F – параметрам горения Чепмена-Жуге с максимальной скоростью D_FО; точка S -  параметрам химпика детонационной волны. Конечное состояние продуктов сгорания в режиме постоянного давления обозначено точкой P, а при мгновенном сгорании в бомбе – точкой V. Состояния в квадранте VOP запрещены для обычных сред, поскольку в этой области расширение вещества должно приводить к увеличению давления. При поджигании смеси скорость распространения пламени (нормальная скорость горения) много меньше скорости D_FО, потому конечное состояние продуктов сгорания во фронте ламинарного пламени с большой точностью соответствует режиму сгорания при постоянном давлении, т.е. точке Р.