Математическая модель управления запасами, синхромаркетинг. Определение режима поставок, страница 6

2.  Каким образом организуется ветвление в задаче выбора

3.  Выполните словесно–формульное описание алгоритма задачи выбора

4.  Спроектируйте блок–схему решения задачи

5.  Изменяя значения параметров в задаче о выборе портфеля заказов, проанализируйте влияние объема ресурсов (A,A_j) и списка заказов на значение f_max и выбор заказов.

11

Лабораторная работа № 4

Комбинаторная задача унификации.

При рассмотрении вопроса о применении различных типов изделий для одной и той же цели, игнорируя условия их производства, возникает задача унификации. При необходимости количества a_i изделий i–го типа, производство их требует затрат f_i(x). Нельзя ли уменьшить затраты за счет уменьшения количества типов изделий (унифицировать их). Электроприборы с меньшей мощностью можно заменить на электроприборы с большей мощности (при этом ухудшаются некоторые показатели, но затраты на производство всех изделий уменьшаются).

Цель задачи: найти минимальные суммарные затраты:

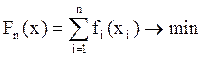                                             (4.1)

при условиях   0 £ x₁,  x₁  £ a₁

0 £ x₂,  x₁+x₂  £ a₁+a₂      и  т.д.

Рассмотрим пример:

Пусть функция затрат имеет вид

                                       (4.2)

Данные сведены в табл. 4.1

                                                                                                  Таблица 4.1

i	ai	bi	ci	fi(ai)
1	5	2	5	15
2	3	2,1	6	12,3
3	4	2,4	8	17,6
4	3	3	10	19
5	5	3,2	11	27
6	2	3,5	13	20
S	22			110,9

Решение задачи представлено на рис. 4.1

На ветвях представлены значения x_i, рядом с вершинами минимальные значения затрат. Жирным цветом отмечены кратчайшие пути.

Минимальные затраты на производство i типов изделий.

                                   (4.3)

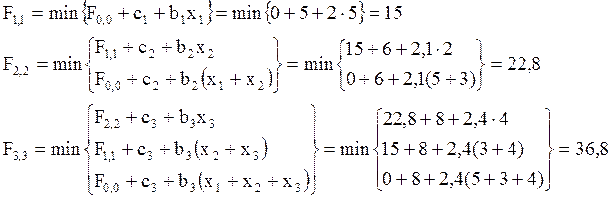
и т.д.

Как видим, имеются два оптимальных решения x=(0;8;0;0;0;14) и x=(0;0;12;0;0;10), отвечающих одному и тому же минимальному значению.

Суммы затрат 84,8 (отличающемуся от начального значения без унификации 110,9 на 23,5%)

12

Рис.4.1

13

Задание.  

Решите задачу унификации для функции

Значения a_i, b_i, c_i заданы в табл.4.2. Определите затраты без унификации. Нарисуйте дерево и расставьте на нем пометки. Результаты проверьте с помощью ППП «Маркетинг».

                                                                                                          Таблица 4.2

i	ai	bi	ci
1	1	2	10
2	3	1	2
3	4	2	8
4	6	3	9
5	2	4	11

Контрольные вопросы:

а) Опишите алгоритм решения задачи унификации.

б) Сколько всего вершин необходимо обработать для нахождения минимальных затрат. Какие особенности задачи сокращают перебор.

в) Сколькими способами можно поставить на шахматную доску 8 фигур?

Лабораторная работа № 5

Сетевые графики и их анализ.

Сетевым графиком называется граф, имеющий одну начальную и одну конечную вершину, направленные дуги (работы), вершины (события), не имеющий внутренних циклов.

Цель задачи: отыскать критический путь и резервы времени, т.к. эти параметры необходимы для оптимизации сетевого графика.