Математическая модель управления запасами, синхромаркетинг. Определение режима поставок, страница 5

Контрольные  вопросы:

1. Сколько вариантов пришлось бы рассмотреть, если требовалось обработать 8 деталей на 2^х станках методом полного перебора

2. Для данных, приведенных в табл.3.1 определите F(p₀), где p₀=(1,2,3,4,5) и сравните с F_min

3. При решении задачи (табл.3.2) в некоторых шагах было 2 одинаковых минимальных элемента. Убедитесь, что выбор другого минимального элемента так же дает оптимальный порядок

4. Рассмотрите задачу упорядочивания, если за пролеживание  i-го объекта взимается штраф a _i.

2. Задача выбора.

Имеется список заказов (i=1,…,N), каждый из которых требует ресурса a_i  и дает прибыль c_i. Данные приведены в табл. 3.3. Каждый заказ может выбираться один раз в единичном количестве. Выберите портфель заказов, чтобы полезность (прибыль) была максимальной.

9

В табл. 3.3 данные уже упорядочены по удельной полезности k_i=c_i/a_{i .}

                                                                                                 Таблица 3.3

i	1	2	3	4	5
ai	5	4	5	4	4
ci	15	12	10	8	8
ki	3	3	2	2	2

Задачу решим методом ветвей и границ (МВГ), основанный на следующих моментах:

1. все множество вариантов представляется в виде графы «Дерево» сужающихся подмножеств, на каждой ветви которого

M^(k) Ì M^(k-1) Ì…ÌM=M⁽⁰⁾ , а конечные вершины отвечают конкретным вариантам

2. на каждом подмножестве вводится мажорирующая функция f и верхняя граница j:

j(x)³f(x)   "   xÎM^(k)

Эффективность метода зависит от того, насколько удачно построено дерево вариантов (такое ветвление, при котором  как можно больше вариантов отсекается на ранних стадиях ветвления и насколько эффективно строятся границы j_M^(k).

Если x_i=0 , то заказ отвергается, если  x_i=1, то заказ принимается. В этом случае задача принимает вид:   a_ix_i  £ A     (ограничение по ресурсам)

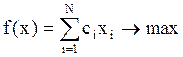 (целевая функция максимизируется).

Ветвление в задаче организуется следующим образом: все множество вариантов М разбивается на два подмножества   М=М₁   È   М_{0 ,}

где М₁ – множество вариантов, отвечающих x₁=1 (т.е. выбору первого заказа), М₀ – множество вариантов, в которых первый заказ не участвует (x₁=0).      

Далее ветвление ведется по x₂ :

M₁=M₁₁ È M₁₀      и       M₀=M₀₁ È M₀₀     и  т.д.

В табл. 3.3 данные упорядочены по удельной полезности, поэтому нужно выбирать максимальное количество первого заказа

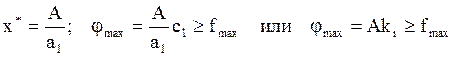
На рис. 3.2 представлено решение задачи МВГ.

В кружке приведена нумерация множества. Отсечение по недопустимости отмечено значком  X, отсечение по условию

отмечено одной косой чертой \ (после получения первого варианта) или двумя косыми чертами \\ (при ветвлении множества после первого отсечения). На рис. 3.2б) вторичные ветвления вынесены отдельно в правую часть рисунка.

Задание.

Решите задачу о выборе портфеля из 8 заказов, ресурсы и прибыль заданы в табл.3.3. Общий объем ресурсов а) 30; б) 25.

 Таблица 3.3

i	1	2	3	4	5	6	7	8
ai	2	5	3	7	3	10	8	11
ci	10	20	12	21	9	20	16	11

Результаты решения проверьте с помощью ППП «Маркетинг».

10

 

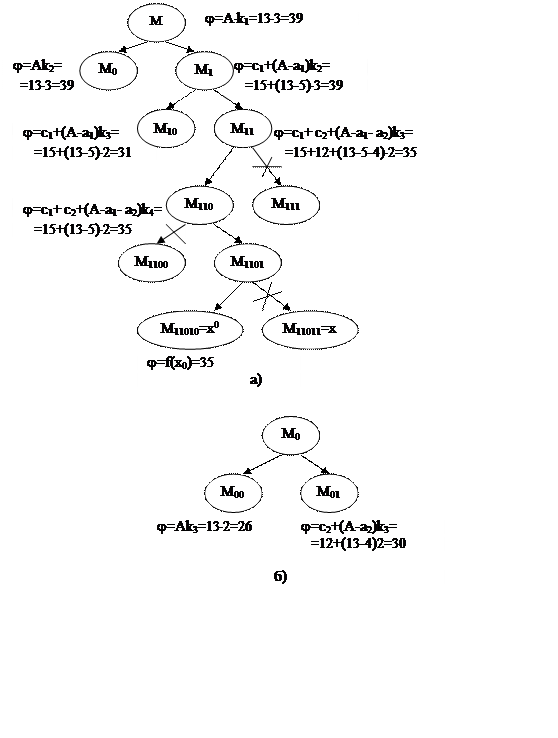Рис.3.2

Контрольные вопросы:

1.  Опишите метод ветвей и границ для решения задачи выбора