Математическая модель управления запасами, синхромаркетинг. Определение режима поставок, страница 4

i	Ci0	Ci	Pi	Si	pi=	Di	di	ri
1	1300	600				0
2	0	500				0
3	0	250	8000			0

Внутренние цены  

P_i=(1+d)C_i+P_i-1+C_i⁰                               (2.3)

Результаты расчета проверьте с помощью ППП «Маркетинг».

Лабораторная работа № 3

Комбинаторные задачи: упорядочивания, выбора.

1. Задача упорядочивания

1.1. Имеется n посетителей, ожидающих приема у директора, и время разговора с каждым из них. Цель задачи – найти такой порядок приема посетителей, при котором суммарное время их ожидания было бы минимальным.

F(p) - min

Порядок оптимален (p = p*), когда посетители упорядочены в порядке возрастания их времен обслуживания         a₁ £ a₂ £…£ a_n

Сумма времен ожидания всех посетителей:

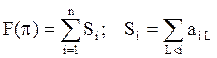                              (3.1)

1.2. Задача двух станков – более сложный вариант задачи упорядочивания. Обрабатываемые объекты последовательно проходят обработку на двух станках (со временем обработки a_i и b_i соответственно). Цель задачи – найти такой порядок их запуска (т.е. перестановку p), при котором время обработки всех объектов на обоих станках и время пролеживания деталей минимально.

Алгоритм решения задачи двух станков:

1. Начало процесса

2. Ввод начальных данных: время обработки деталей на каждом станке  a_i и b_i , i=1,…,n

3. Организация цикла по множеству деталей j=1,…,n  (т.е. формируется очередь обработки)

4. Поиск детали, имеющей наименьшее время обработки                                                                                                           

5. Если наименьшее время обработки первым станком t=a_i0, то реализуется неравенство  ai £ bi , a_j £ b_j , a_i £ b_j  и деталь i₀ добавляется в очередь сначала, иначе реализуется условие   a_i £ b_i , a_j > b_j или a_i  ³ b_i , a_j  ³ b_j , a_j > b_i   и деталь добавляется в очередь с конца.              

6. Удаление детали из множества

7. Конец цикла

8. Вывод результата: последовательность обработки деталей

9. Конец процесса

Рассмотрим пример. Данные приведены в табл. 3.1

Таблица 3.1

i	1	2	3	4	5	S
ai	6	4	1	2	3	16
bj	4	3	2	6	6	20

8

Согласно алгоритму находим

i₀=3        (a_i0=1)          *=(3,…)

i₀=4        (a_i0=2)          *=(3,4,…)

i₀=5        (a_i0=3)          *=(3,4,5,…)

i₀=2        (b_i0=3)          *=(3,4,5,…2)

i₀=1        (b_i0=4)          *=(3,4,5,1,2)

График занятости станков при таком порядке обработке деталей приведен на рис. 3.1, откуда следует, F_min=F(p*)=22

Рис. 3.1

Задание.

Определите оптимальную последовательность обработки 10 деталей на 2^х станках. Нарисуйте график занятости станков и определите минимальное суммарное время обработки. Время обработки задано в табл. 3.2. Результаты решения проверьте с помощью ППП «Маркетинг».                                                                                                                 

Таблица 3.2

i	1	2	3	4	5	6	7	8	9	10
ai	2	8	14	3	6	11	45	2	14	6
bj	5	8	26	43	1	13	9	20	4	7