Основные фонды предприятий, объем произведенной продукции, средняя численность рабочих. Данные по предприятиям города

Задача №1

Таблица 6 - Данные по предприятиям города:

№	Средняя списочная численность рабочих, чел.	Среднегодовая стоимость основных фондов, млн.р.	Объем произведенной продукции за год, млн.р.
1	100	369	56000
2	140	473	7500
3	94	251	2500
4	83	280	3800
5	157	590	9450
6	195	1200	20800
7	54	160	1280
8	120	480	5760
9	180	970	15030
10	125	400	6440
11	45	120	720
12	256	900	14400
13	182	670	670
14	124	500	7000
15	110	379	6000
16	102	256	3100
17	96	220	3700
18	98	240	3500
19	84	126	800
20	76	180	1600
21	96	250	3200
22	85	230	3000
23	110	370	5800
24	112	350	6300
25	67	125	850
26	63	140	1300
27	250	1150	19900
28	212	790	12200
29	184	290	3400
30	137	275	4200

Проведите структурную группировку предприятий по величине среднегодовой стоимости основных фондов. Укажите, какая группа является наиболее типичной. Постройте график зависимости между объемом произведенной продукции и среднегодовой стоимостью основных фондов. Проведите анализ полученных результатов.

Решение:

1. Построим структурную группировку. В качестве группировочного признака возьмем величину среднегодовой стоимости основных фондов. Образуем шесть групп с равными интервалами. Величину интервала определим по формуле:

h = ;

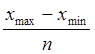h=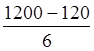180.

Обозначим границы групп:

1 группа 120-300

2 группа 300 – 480

3 группа 480-660

4 группа 660-840

5 группа 840-1020

6 группа 1020-1200

Таблица 2 - Разработочная таблица

Группа	Среднегодовая стоимость	Средняя стоимость	Объём производства	Численность
1	120 - 300	251 160 120 256 220 240 126 180 250 230 125 140 290 275 280	2500 1280 720 3100 3700 3500 800 1600 3200 3000 850 1300 3400 4200 3800	94 54 45 102 96 98 84 76 96 85 67 63 184 137 83
2	300 - 480	369 473 480 400 379 370 350	56000 7500 5760 6440 6000 5800 6300	100 140 120 125 110 110 112
3	480 - 660	590 500	9450 7000	157 124
4	660 - 840	670 790	670 12200	182 212
5	840 - 1020	970 900	15030 14400	180 256
6	1020 - 1200	1200 1150	20800 19900	195 250
	ВСЕГО:	12734	230200	3737

Результаты группировки записываются в сводную таблицу:

Таблица 3 – Группировка банков региона по среднегодовой стоимости основных фондов

Группа	Среднегодовая стоимость	Средняя стоимость	Объём производства	Численность
1	120 - 300	3143	36950	1364
2	300 - 480	2821	93800	817
3	480 - 660	1090	16450	281
4	660 - 840	1460	12870	394
5	840 - 1020	1870	29430	436
6	1020 - 1200	2350	40700	445
	Итого:	12734	230200	3737

Данные, приведенные в таблице 3, показывают, что в основном в городе преобладает 1 группа с наибольшей среднегодовой стоимостью основных фондов. Для большей наглядности и выявления закономерностей распределения банков по величине уставного капитала результаты проведенной группировки можно заменить на относительные показатели структуры.

Таблица 4 - Группировка банков региона по среднегодовой стоимости основных фондов.

Группа	Средняя стоимость	Средняя стоимость к общему, %	Объём к общему,%	Численность,%
1	120-300	24,6819	16,0512	36,4998
2	300-480	22,1532	40,7471	21,8624
3	480-660	8,5597	7,1459	7,5194
4	660-840	11,4653	5,5907	10,5432
5	840-1020	14,6850	12,7845	11,6671
6	1020-1200	18,4545	17,6802	11,9079
	Итого:	100	100	100

Группа	Средняя численность		Стоимость			Мощность
			Всего		На 1 человека	Всего	На 1 человека
1	120 – 300		3143		4,05	36950	6,23
2	300 - 480		2821		4,51	93800	2,45
3	480 - 660		1090		11,68	16450	13,9
4	660 – 840		1460		8,72	12870	17,8
5		840-1020		1870	6,80	29430	7,82
6		1020-1200		2350	5,41	40700	5,65
		Итого:		12734		230200

Вывод: Из таблицы видно, что с увеличением стоимости основных фондов на 1 человека, увеличивается мощность. Это говорит о наличии прямой связи между рассматриваемыми признаками.

Задача №13.

Таблица 15 - Данные о забастовках в РФ:

Год	Число организаций, на которых проходили забастовки	Численность работников, участвовавших в забастовках, тыс. чел.	Количество времени, не отработанными участвовавшими в забастовках работниками, тыс. чел.-дн.
1992	6273	357,6	1893,3
1997	17007	887,3	6000,5
2001	291	13,0	47,1

Рассчитайте для каждого года среднюю численность работников, участвовавших в забастовках, в расчете на одну организацию, средние потери рабочего времени в расчете на одну организацию.

Решение:

а) Средняя численность работников, участвовавших в забастовках, в расчете на одну организацию:

1992: 357600 / 6273 = 57 чел.

1997: 887300 / 17007 = 52 чел.

2001: 13000 / 291 = 45 чел.

б) Средние потери рабочего времени в расчете на одну организацию:

1992: 1893300 / 6273 = 301 чел.-ден.

1997: 6000500 / 17007 = 353 чел.-ден.

2001: 47100 / 291 = 162 чел.-ден.

Задача №18

Выборочное 5%-ное обследование размеров домохозяйств района, проведенное на основе собственно-случайного бесповторного отбора, позволило получить следующие данные:

Таблица 24

Размер домохозяйства, чел.	1	2	3	4	5	6	7
Число домохозяйств	35	94	167	53	12	4	1

С вероятностью 0,954 определите границы среднего размера домохозяйства, границы общей численности населения района.

Размер домохозяйств	Число домохозяйств	xf	X2f
1 2 3 4 5 6 7	35 94 167 53 12 4 1	35 188 501 212 60 24 7	35 376 1503 848 300 144 49
	366	1027	3255

X = 1027/366 = 2,8

2,8-0,08<Х<2,8+0,08

Ответ: Граница среднего размера домохозяйств, представляет собой:

Задача №23

Таблица 30 - Количество проданных автомобилей в регионе

В тысячах штук

1996	1997	1998	1999	2000
500	480	490	450	460

Определите: цепные и базисные: абсолютные приросты; темпы роста; темпы прироста; абсолютное значение 1% прироста;  средний уровень ряда, среднегодовой абсолютный прирост среднегодовой темп роста, среднегодовой темп прироста.

Абсолютный прирост цепной

∆yц = yi – yi-1.

∆yц = 480 – 500 = -20

490 – 480 = 10

450 – 490 = -40

460 – 450 = 10

Абсолютный прирост базисный.

∆yб= yi – y0.

∆yб = 480 – 500 = -20

490 – 500 = -10

450 – 500 = -50

460 – 500 = -40

Цепной темп роста.

Tpц = yi/yi-1 * 100

Tpц = 480/500 * 100 = 96

490/480 * 100 = 102

450/490 * 100 = 92

460/450 * 100 = 102

Базисный темп роста:

Tpб = yi/y0 *100

Tpб = 480/500 * 100 = 96

490/500 * 100 = 98

450/500 * 100 = 90

460/500 * 100 = 92

Цепной темп прироста.

Тпрц =  yi - yi-1/ yi-1 * 100

Тпрц = -20/500 * 100 = -4

10/480 * 100 = 2

-40/490 * 100 = -8

10/450 * 100 = 2

Базисный темп прироста.

Тпрб = yi - y0/ y0 *100

Тпрб =  -20/500 * 100 = -4

-10/500 * 100 = -2

-50/500 * 100 = -10

-40/500 * 100 = -8   

Абсолютное значение одного процента прироста.

AI% = ∆y/Тпр

AI% = -20/4 = 5

10/2 = 5

-40/-8 = 5

10/2 =5

Средний уровень интервального ряда.

Y= y1+y2+…yn / n = 2380/5 = 476

Средний абсолютный прирост.

= yn – y₁ / n – 1 = 460 – 500/ 4 = -10

Средний темп роста

= = 140,7

Средний темп прироста

= -100% = 140,7 – 100 = 40,7

наименование показателя	условное обозначение	период времени
		1996	1997	1998	1999	2000
абсолютные уровни	уi	500	480	490	450	460
абсолютный цепной прирост	∆уц		-20	10	-40	10
абсолютный базисный прирост	∆уб		-20	-10	-50	-40
цепные темпы роста	Трц		0.96	1.02	0.92	1.02
базисные темпы роста	Трб		0.96	0.98	0.9	0.92
цепные темпы прироста	Тпрц		-4	2	-8	2
базисные темпы прироста	Тпрб		-4	-2	-10	-8
содержание одного % прироста	А1%		5	5	5	5
средний уровень ряда		476
средний абсолютный прирост		-10
Средний темп роста		104.7
средний темп прироста		40.7

Вывод: В результате проведенных расчетов, мы получили, что  абсолютные приросты в основном отрицательные. Темпы роста в общем меньше единицы, темпы прироста, абсолютное значение 1% прироста в общем больше единицы. Средний абсолютный прирост отрицательный  и средний темп прироста положительный. Это свидетельствуют о том, что в общем численность страны увеличилась.

Задача №28

Таблица 36 - Реализация товара на трех рынка города:

Найдите сводные индексы цен, физического объема, товарооборота, абсолютную величину изменения товарооборота за счет действия разных факторов.

Индекс товарооборота равен:

I_pq = 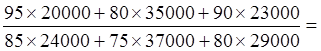 0,9488

Индекс физического объема по Ласпейресу равен:

I_q = 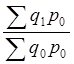 = = 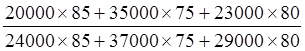0,8640

Индекс цен рассчитывается по формуле Паше:

I_p = 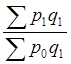 =  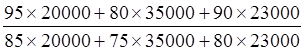= 1,0981

Абсолютную величину изменения товарооборота за счет действия разных факторов, получим как разность числителя и знаменателя индекса цен:

 == 6770000 – 6165000 = 605000

Ответ: Уменьшение товарооборота составило 5,12% (94,88 – 100), физический объем реализации уменьшился на 13,6% (86,40 – 100), цены выросли на 9,81% (109,81 – 100). Абсолютная величина изменения товарооборота за счет действия разных факторов равна 605000р