15,9966; 16,0001; 15,9944; 15,9973; 15,9989; 15,9951.
Обработаем массив экспериментальных данных, определив оценки числовых характеристик и построим гистограмму
Данный массив данных представлю в виде таблицы 3:
Таблица 3
|
Интервал измеренных значений, мА |
Число значений в интервале |
|
15,9903 … 15,9921 |
1 |
|
15,9921… 15,9939 |
2 |
|
15,9939 … 15,9957 |
5 |
|
15,9957 … 15,9975 |
7 |
|
15,9975 … 15,9993 |
2 |
|
15,9993 … 16,0012 |
1 |
На основании экспериментальных данных построю гистограмму (рис. 10), используя правила построения гистограмм.
![]()
![]()
рис.10. Гистограмма, построенная по экспериментальным данным.
По виду представленной диаграммы можно выдвинуть гипотезу о том, что результат измерения подчиняется нормальному закону распределения вероятности. Поскольку n = 18, для проверки гипотезы о нормальности закона распределения вероятности результата измерения используется составной критерий. В этом случае необходимо рассчитать:
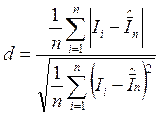 (4)
(4)
Результаты вспомогательных вычислений сведены в табл.4
Таблица 4
|
, мА |
, мА |
, |
|
1 |
2 |
3 |
|
15,9941 |
- 0,0018 |
0,00000324 |
|
15,9960 |
0,0001 |
0,00000001 |
Продолжение таблицы 4
|
1 |
2 |
3 |
|
15,9962 |
0,0003 |
0,00000009 |
|
15,9930 |
- 0,0029 |
0,00000841 |
|
15,9956 |
- 0,0003 |
0,00000009 |
|
15,9911 |
- 0,0048 |
0,00002304 |
|
15,9932 |
- 0,0027 |
0,00000729 |
|
15,9981 |
0,0022 |
0,00000484 |
|
15,9974 |
0,0015 |
0,00000225 |
|
15,9970 |
0,0011 |
0,00000121 |
|
15,9958 |
- 0,0001 |
0,00000001 |
|
15,9959 |
0,0000 |
0,00000000 |
|
15,9966 |
0,0007 |
0,00000049 |
|
16,0001 |
0,0042 |
0,00001764 |
|
15,9944 |
- 0,0015 |
0,00000225 |
|
15,9973 |
0,0014 |
0,00000196 |
|
15,9989 |
0,0030 |
0,0000090 |
|
15,9951 |
- 0,0008 |
0,00000064 |
|
|
|
|
На основании выполненных расчётов d = 0,748 .
![]() Согласно табл.11 (Шишкин
И.Ф. Теоретическая метрология) условие
Согласно табл.11 (Шишкин
И.Ф. Теоретическая метрология) условие ![]() соблюдается
с вероятностью .
соблюдается
с вероятностью .
При n =18 не
более одного результата измерения![]() c вероятностью 0,98 может отличаться
от среднего арифметического значения
c вероятностью 0,98 может отличаться
от среднего арифметического значения ![]() больше,
чем на
больше,
чем на ![]() .
.
Так как 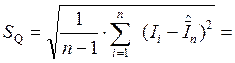 0,0022
мА , (5)
0,0022
мА , (5)
то из второго столбца таблицы следует, что ни один результат
измерения ![]() не отличается от
не отличается от ![]() больше,
чем на
больше,
чем на ![]() .
.
Следовательно, гипотеза о нормальности закона распределения вероятности результата измерения может быть принята с вероятностью
Р = 0,99+0,98-1=0,97
Выражение для плотности распределения вероятности результата измерения, подчиняющегося нормальному закону, имеет вид:
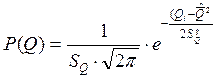 , (6)
, (6)
при ![]() получим
получим 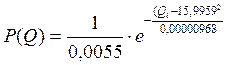 ,
,
Результаты расчёта Р(Q) сведены в табл.5:
Таблица 5
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.