Применение прямых методов к решению краевых задач для обыкновенных дифференциальных уравнений (ОДУ), Метод Ритца

Применение прямых методов к решению краевых задач для обыкновенных дифференциальных уравнений (ОДУ). Метод Ритца

Суть прямых методов: краевые задачи для ОДУ сводятся к решению вариационной задачи, ищется в виде отрезка ряда, который при увеличении количества слагаемых сходится к точному решению.

Необходимо решить уравнение:

Рассмотрим обычное дифференциальное уравнение второго порядка:

1.  Необходимо ввести новую переменную, которая позволяет удовлетворить граничным условиям.

Запишем систему линейных уравнений относительно неизвестных параметров а и  b:

Если     ,                                          

,                                        

      →  →

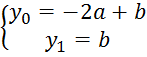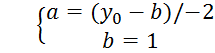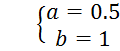
2.  Рассмотрим граничную задачу, которую сводим к стандартному виду:

Введем функцию  

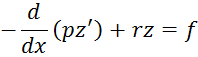
Решение данной краевой задачи равносильно минимизации функционала

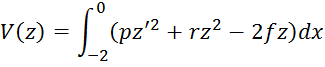
Воспользуемся методом Ритца для построения приближенного решения краевой задачи. Функцию z(x), входящую в состав функционала аппроксимируем в отрезок  ряда:

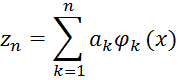
Отрезок ряда  z_nдолжен удовлетворять граничным условиям:

Это можно сделать в результате выбора функции :

В соответствии с заданным условием найдем:

Запишем разрешающую систему, которая имеет следующий вид:

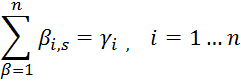
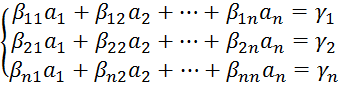
ищем в виде:

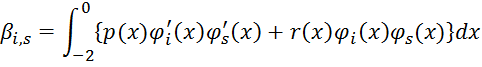
находим следующим образом:

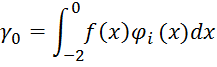
Необходимые вычислительные операции выполнены с помощью программы Mathcad и представлены ниже:

Найденныеzзанесем в таблицу:

x/z	z₂	z₃	z₄
-0.4	-0.16997	0.10849	0.11082	0.11065	0.00017
-0.8	-0.03732	-0.02326	-0.02689	-0.02756	0.00066
-1.2	-0.13475	-0.09715	-0.09949	-0.09881	0.00068
-1.6	0.002748	-0.25435	-0.25629	-0.25591	0.00038

Неравенство выполняется, соответственно -  это решение.