Ресурс всей плазменной установки определяется ресурсом, а следовательно надежностью и прочностью различных систем: электропитания, запуска и автоматики, систем подачи и хранения рабочего тела, вспомогательных систем и собственно ускорителя плазмы или технологического плазменного устройства и равен меньшему из ресурсов систем, если не используется резервирование наименее надежных систем.
Ресурс непосредственно плазменного ускорителя или технологического плазменного устройства зависит от стойкости изоляторов, электродов и других вспомогательных элементов. Не последнюю роль здесь играют и температурные напряжения, возникающие в электродах.
Расчет пластинчатых электродов ионно-оптической системы на прочность состоит из двух частей. В первой части находится напряженное и деформированное состояние электрода, вызванное его неравномерным по радиусу нагревом. Во второй анализируются условия, обеспечивающие сохранение электродом первоначальной формы при нагревании и длительной работе. Рассмотрим первую задачу.
Схема электрода показана на рис. 1. Электрод состоит из перфорированной пластины, являющейся собственно электродом, и силового кольца, которым электрод крепится к фланцу. На рисунке показана эпюра температур электрода при установившейся работе ускорителя. Неравномерный нагрев электрода вызывает температурные напряжения. Как видно из рисунка, температура средней части выше, чем периферийной, что может привести к выпучиванию электрода.
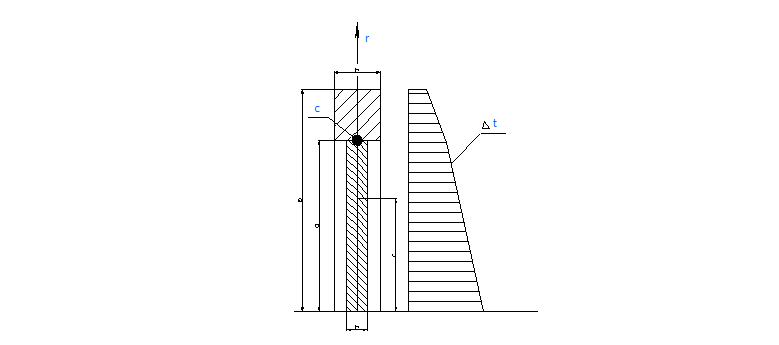 Рис.
1 - Схема электрода
Рис.
1 - Схема электрода
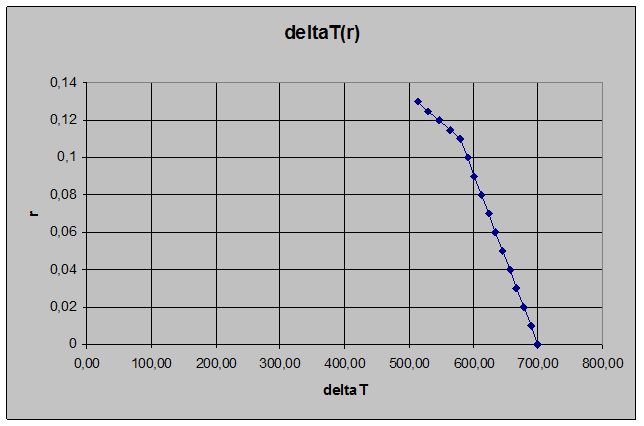
Рис. 2 - Распределение температур по радиусу
Исходные данные для расчета:
·
Коэффициент линейного расширения материала электрода(Мо), 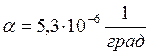 ;
;
·
Коэффициент линейного расширения материала кольца(сталь Х18Н10Т),
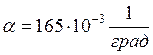 ;
;
·
Модуль упругости материала электрода для данного изменения
температур, ![]() ;
;
·
Модуль упругости материала кольца для данного изменения
температур, ![]() ;
;
·
Коэффициент Пуассона ![]() ;
;
·
Градиент температур по радиусу сетки 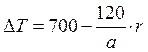
·
Градиент температур по радиусу кольца 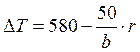
· Радиус сетки электрода, а=110мм;
· Радиус кольца b=125мм;
· Толщина электрода h=1мм;
· Толщина кольца hк=5мм.
Итак, известны h, hк, ΔT, E, α. Требуется определить σr, σφ.
Основным осложнением при определении напряженного состояния электрода является существенное различие в толщинах собственно электрода и его силового кольца. На стыке этих двух элементов возникают силы реакции R, которые следует определить. Необходимо также при определении напряжений в электроде учитывать ослабление его отверстиями.
Определим сначала градиент температур по радиусу сетки
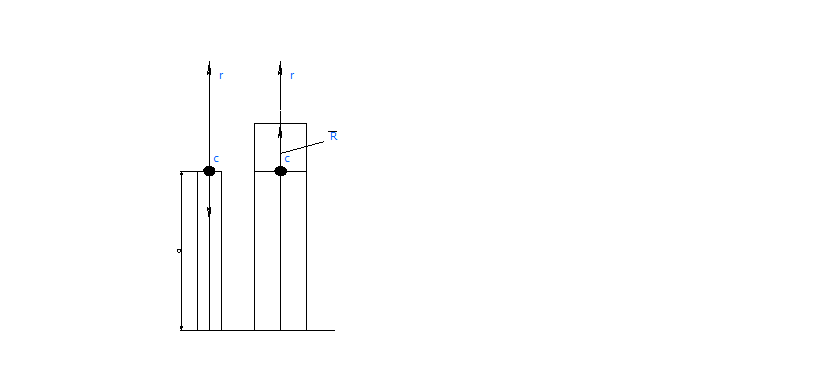 Рис. 3
- Схема нагружения электрода
Рис. 3
- Схема нагружения электрода
Находим значение этой силы из условия равенства радиальных деформаций кольца Ukа и электрода Uа на радиусе а:
![]() (1)
(1)
![]() (2)
(2)
где eа,, ekа – податливость электрода и кольца в точке С от распределенной контурной нагрузки;
eао, ekао – податливость электрода и кольца от внешней нагрузки;
Po, Pko - внешняя нагрузка на электрод и кольцо.
В рассматриваемом случае внешней нагрузкой является нагрев до температуря t, а произведение eао Po – температурная деформация электрода в точке С; аналогично, ekао Pko – температурная деформация кольца в точке С. Учтем, что
![]() =R/(2πC)
=R/(2πC)
Из условия равенства Uа=Ukа получим:
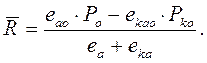 (3)
(3)
Все величины, входящие в числитель формулы (3), известны:
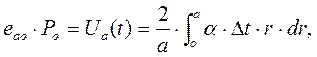 (4)
(4)
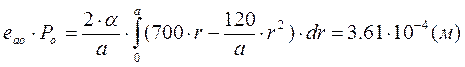 ,
,
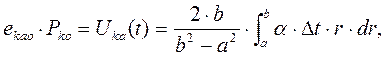 (5)
(5)
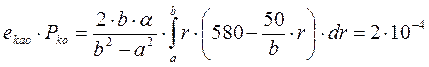 (м)
(м)
Податливость eа, ekа , входящие в знаменатель формулы (6.5), найдем из рис. 4
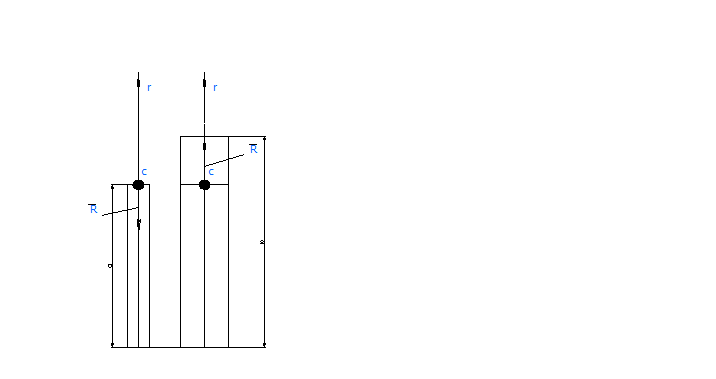 Рис. 4
- Модель электрода
Рис. 4
- Модель электрода
Если приложить распределенное усилие ![]() к
радиусу а электрода, то податливостью последнего будет называться
соотношение:
к
радиусу а электрода, то податливостью последнего будет называться
соотношение:
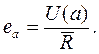 (6)
(6)
Удлинение электрода на радиусе а от нагрузки ![]()
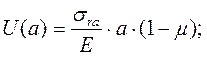 (7)
(7)
откуда
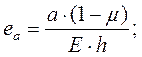 (8)
(8)
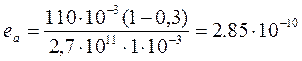 м;
м;
аналогично, податливость кольца
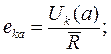 (9)
(9)
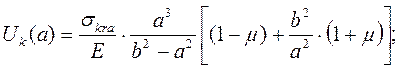 (10)
(10)
и окончательно
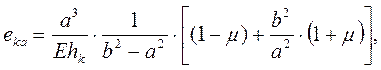 (11)
(11)
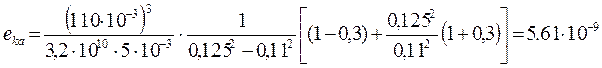 м, где h и hk
– толщины электрода и кольца.
м, где h и hk
– толщины электрода и кольца.
Зная необходимые величины подставим их в формулу (3), определим:
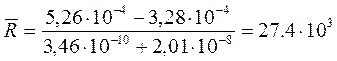 Н.
Н.
Найдем напряжения в электроде и кольце от нагрузки ![]() :
:
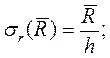 (12)
(12)
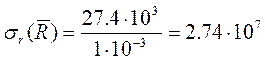 Па;
Па;
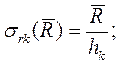 (13)
(13)
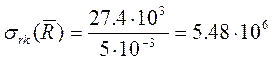 Па;
Па;
![]() (14)
(14)
![]() Па;
Па;
![]() (15)
(15)
![]() Па.
Па.
Напряжения в электроде определяются по формулам:
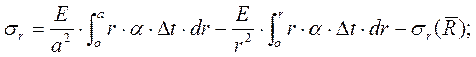
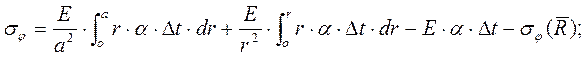 (17)
(17)
Проведем расчет на нескольких радиусах, а результаты сведем в таблицу 1:
Табл. 1 - Распределение напряжений по радиусу сетки
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.