Примеры расчетов элементов фотоэлектрической батареи, страница 6

где     ;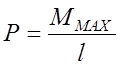

l – плечо.

Значит,

,

(8.3.44)

отсюда

.

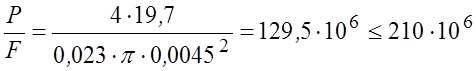Таким образом, ось диаметром 4,5 мм выдержит данную нагрузку.

Определим надежность узла крепления панели (замка).

Таким образом,

(8.3.45)

Вероятность безотказной работы вычислим по выражению

,

(8.3.46)

где 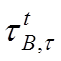     - предел длительной прочности (справочная величина);

 - максимально действующее напряжение;

 - дисперсия допустимых значений предела длительной прочности (справочная величина);

 - дисперсия допустимых значений максимально действующего напряжения:

	(8.3.47)
	(8.3.48)

(8.3.49)

Подставив значения систем (8.3.48) и (8.3.49) в выражение (8.3.47), найдем значение дисперсии допустимых значений максимально действующего напряжения .

Подставив значение  и  в выражение (8.3.46), определим вероятность безотказной работы.

8.3.6  Основы расчета приводов механизма ориентации фотоэлектрической батареи

8.3.6.1  Расчет на прочность цилиндрической ступени редуктора

Проведем проверочный расчет первой цилиндрической ступени редуктора на контактную выносливость и изгибную выносливость. Параметры ступени:

-  передаточное отношение U =2.5;

- частота вращения шестерни 6000 об/мин;

- частота вращения колеса 2400 об/мин;

- момент на валу шестерни 0.08 Н·м;

- число зубьев шестерни =40, =100;

-  модуль зацепления m=0,3 мм;

-  делительный диаметр шестерни =12 мм; колеса =30 мм;

-  материал: сталь 45; твердость поверхности 40HRC.

8.3.6.2  Расчет на контактную выносливость активных поверхностей зубьев

Расчетное контактное напряжение в полюсе зацепления для цилиндрических передач

(8.3.50)

где      - коэффициент, учитывающий форму сопряженных поверхностей зубьев;

 – коэффициент, учитывающий механические свойства материалов сопряженных колес;

 – коэффициент, учитывающий суммарную длину контактных линий (для прямозубых цилиндрических передач =1);

 – удельная расчетная окружная сила, Н/мм:

(8.3.51)

Здесь       - коэффициент расчетной нагрузки;

 – коэффициент, учитывающий неравномерности распределения нагрузки по длине контактных линий;

 – коэффициент динамической нагрузки;

 – крутящий момент на шестерне, Н×м;

b – ширина зубчатого венца, мм;

 – диаметр шестерни, мм;

u– передаточное отношение.

,

(8.3.52)

где =0 – угол наклона зубьев, град;

= – угол зацепления.

(8.3.53)

где      МПа – приведенный модуль упругости для стальной шестерни и колеса;

= 0.3 – коэффициент Пуассона.

Удельная окружная динамическая сила, H/мм:

,

(8.3.54)

где     = 0.04 – коэффициент, учитывающий влияние вида зубчатой передачи и модификации профиля зуба;

 = 0.38 м/c – коэффициент, учитывающий влияние разности основных шагов зацепления зубьев шестерни и колеса.

(8.3.55)

Тогда

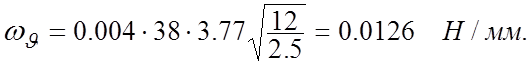
Удельная полезная окружная сила в зоне ее наибольшей концентрации

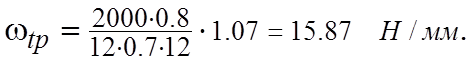
Коэффициент расчетной нагрузки

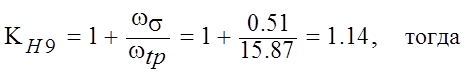
Получим расчетную удельную окружную силу

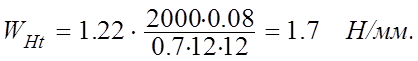
Тогда расчетное контактное напряжение

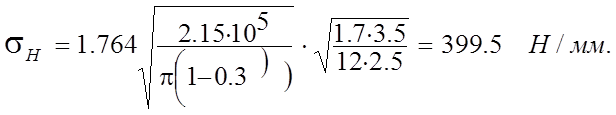
Допускаемые контактные напряжения

=18HRC+150=18·40+150=870 МПа, а с учетом долговечности  и коэффициента безопасности  имеем

 0.9·870/1.1=710  МПа.

Коэффициент запаса .

8.3.6.3  Проверка зубьев передачи на изгибную выносливость

Назначение расчета – предотвращение усталостного излома зубьев. Расчетное напряжение для цилиндрических колес, МПа:

,

(8.3.56)

где – коэффициент формы зуба , =3.93 для ;

 – коэффициент, учитывающий перекрытие зубьев. Принимаем =4 для ;

 – коэффициент, учитывающий наклон зубьев, для прямозубых передач=1;

m – модуль зацепления, мм.

Удельная расчетная окружная сила вычисляется так же, как сила при расчете зубьев на контактную выносливость, но значение коэффициента расчетной нагрузки иное:

,

(8.3.57)