Примеры расчетов элементов фотоэлектрической батареи, страница 5

где      - предел изгибной выносливости, МПа;

 - коэффициент безопасности;

=0,9 - коэффициент долговечности.

При твердости HRC40 - =800 МПа, =2,2, тогда

 МПа<  МПа.

Коэффициент запаса К_з=1,34.

8.3.4  Расчет на прочность торсиона

При раскрытии БФ следует просчитать торсион каждой панели БФ на прочность.

Исходные данные при расчетах:

-  материал торсиона – сталь 65Г;

-  модуль сдвига – G=8,1·10¹⁰ Па;

-  допустимые напряжения при кручении -  Па.

Угол закрутки торсиона определяется формулой

,

(8.3.21)

где     М_кр – момент закрутки торсиона;

l – длина торсиона;

G – модуль сдвига;

J_р– момент инерции сечения торсиона при кручении.

Уравнение движения панели при раскрытии:

,

(8.3.22)

где     t – время раскрытия (поворота) панели,

e - угловое ускорение панели из уравнения движения вращающегося тела:

.

(8.3.23)

Здесь J_n– момент инерции панели.

Таким образом, уравнение движения панели будет иметь вид

.

(8.3.24)

Приравнивая правые части уравнений (8.3.23) и (8.3.24), получаем

,

(8.3.25)

или

.

(8.3.26)

Отсюда видно, что время раскрытия панели не зависит от величины момента, отдаваемого торсионом.

При заданной длине торсиона можно определить его жесткость

,

(8.3.27)

где     J_n=bhb³ (h – большая сторона торсиона; b– меньшая сторона торсиона; b=f(h/b) – табличная величина).

Отсюда

.

(8.3.28)

Задав ширину торсиона h=0,014 м; время раскрытия t=5 с; длину торсиона l=1,09 м, вычисляем

,

(8.3.29)

где     m – масса панели;

H=1,33 м – ширина панели.

Массу панели вычислим по формуле

,

(8.3.30)

где r=7,8×10³ кг/м³ - плотность стали;

V – объем используемой в конструкции БФ стали:

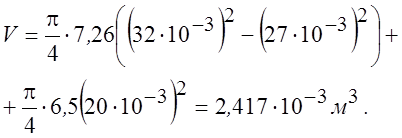
тогда     кг.

Таким образом, момент инерции панели

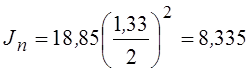 кг·м².

Приняв b=0,313, вычисляем толщину торсиона

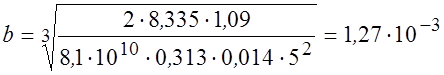 м,

тогда 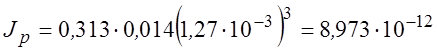 м⁴.

При закрутке торсиона на 180° (полностью сложенные панели БФ) крутящий момент имеет вид

;

(8.3.31)

Момент сопротивления при кручении

,

(8.3.32)

где     a=f(h/b) – табличная величина,

 м³.

Максимальные касательные напряжения, возникающие при закручивании торсиона, определяем по формуле

(8.3.33)

где     g=f(h/b) – табличная величина.

Для равномерного раскрытия момент на последнем (ближнем к корпусу ЛА) торсионе должен быть в четыре раза больше чем на первом. Этот момент определим как

,

(8.3.34)

Зная величину момента кручения , определим толщину последнего торсиона

(8.3.35)

Момент сопротивления сечения торсиона

 Па.

Максимальные напряжения, возникающие при закрутке торсиона:

.

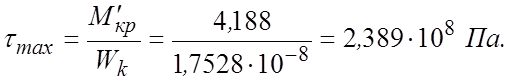
(8.3.36)

Коэффициент запаса

(8.3.37)

8.3.5  Расчет на прочность замка

Максимальную нагрузку в узле крепления будет испытывать ось замка 1 при раскрытии панели (рис. 8.10). Схема раскрытия панелей показана на рис. 8.11.

Пружина в узле раскрытия подобрана так, чтобы время раскрытия панелей было около двух минут. Тогда угловая скорость

с-1.

(8.3.38)

Изгибающий момент рассчитаем по формуле

,

(8.3.39)

где     L – длина панели;

Е – модуль упругости;

m – погонная масса панели;

I – момент инерции сечения панели:

.

(8.3.40)

Здесь a=0,79 м – ширина панели;

b=0,017 м – толщина панели.

Тогда

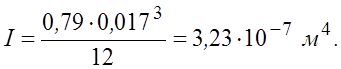
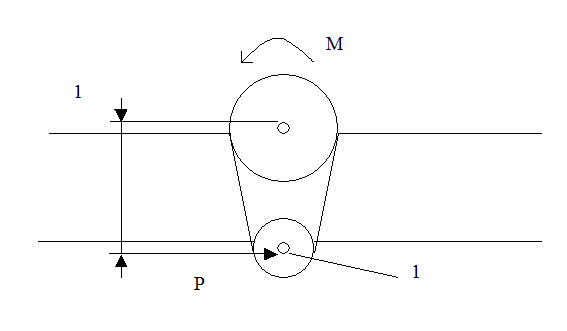
Рис. 8.10 Схема замка панели

Найдем погонную массу m по формуле (8.3.41):

,

(8.3.41)

где     m_п – масса панели;

L – длина панели.

Рис. 8.11 Схема раскрытия панелей

Тогда

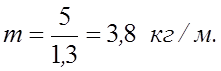
Итак,

Запишем условие прочности при сдвиге:

,

(8.3.42)

где      Н/м².

Схема панели показана на рис. 8.12.

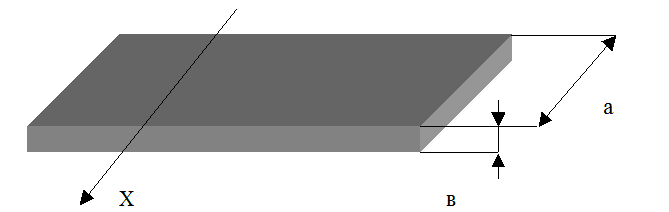
Рис. 8.12 Схема панели

При круглом сечении

,

(8.3.43)