Законы Кирхгофа. Первый закон Кирхгофа

Билет №5

Законы Кирхгофа

Первый закон Кирхгофа

Первый закон Кирхгофа, вытекающий из принципа непрерывности электрического тока (т. е. в узлах невозможно накопление зарядов), при­меняется к узлу электрической цепи, например к узлу а (рис. 3.4). Первый закон Кирхгофа формулируется следующим образом: алгебраическая сум­ма токов в узле равна нулю.

∑I_i = 0.                                       (3.5)

Знаки токов берутся в зависимости от их направления в схеме относи­тельно узла, для которого написан первый закон Кирхгофа. Токам, направлен­ным к узлу, приписывается одинаковый знак, например «минус»; тогда токам, направленным от узла, - «плюс». Такой выбор знаков соответствует аналитиче­скому выражению тока, описанному вектором плотности тока сквозь замкнутую поверхность, где токи, направленные из поверхности наружу, получаются по­ложительными, а токи, направленные внутрь поверхности, - отрицательными.

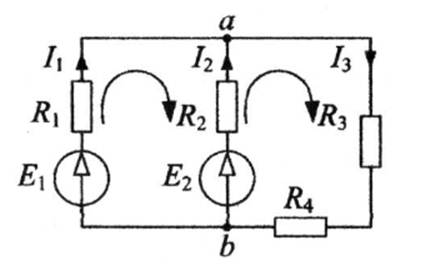Рис. 3.4. Электрическая цепь с двумя источниками ЭДС

Запись уравнений имеет следующие разновидности:

• общая:

∑_i=1ⁿ I_i;

• в развернутой форме, например для узла а:

(-I₁-I₂+I₃)=0;

• в виде соотношения между токами:

(I₃=I₁+I₂).

Второй закон Кирхгофа

Второй закон Кирхгофа является следствием закона сохранения энер­гии и применяется для замкнутых контуров разветвленной цепи (см. рис. 3.4).

Этот закон формулируется следующим образом: алгебраическая сумма ЭДС в любом контуре электрической цепи равна алгебраической сумме падений напряжений на сопротивлениях, входящих в этот контур.

∑E_i - ∑U_i  = 0;

или

∑_i=1ⁿE_i = ∑_j=1ⁿU_j ,

где   ∑_i=1ⁿE_i и ∑_j=1ⁿU_j - алгебраические суммы соответственно ЭДС источников и падений напряжений на пассивных элементах цепи (сопро­тивлениях резисторов и внутренних сопротивлениях источников ЭДС, содержащихся в рассматриваемом контуре).

Применяется и другая формулировка второго закона: алгебраическая сумма напряжений в любом контуре равна нулю.

∑_s=1ⁿUs = 0,                                (3.7)

где   ∑_s=1ⁿUs - алгебраическая сумма падения напряжений на пассивных

элементах цепи и напряжений на зажимах источников ЭДС, содер­жащихся в рассматриваемом контуре.

При составлении уравнений для расчета электрических цепей по второму закону Кирхгофа необходимо знать направления ЭДС Е и тока J источников электрической энергии, а также положительные направления токов I и падения напряжений U на участках внешней части цепи. Поло­жительное направление ЭДС Е источника указывает направление возрас­тания потенциала внутри источника. Поэтому на электрической схеме оно обозначается стрелкой от зажима, имеющего более низкий потенциал («минус»), к зажиму, имеющему более высокий потенциал («плюс»). Со­ответственно берется и положительное направление тока J (см. п. 1.1) ис­точника тока. На отдельных участках (ветвях) контуров разветвленной цепи (см. рис. 3.4) протекают различные по модулю и знаку токи - в отли­чие от неразветвленной цепи. Поэтому при составлении уравнений по второму закону Кирхгофа должны быть заданы направления токов в вет­вях. Это могут быть направления действующих токов I в ветвях, равных токам I источников тока в этих ветвях. Если же направления токов в вет­вях схемы заранее неизвестны, то их выбирают произвольно и условно считают положительными, подразумевая именно условное положитель­ное, а не действительное направление тока. Положительные направления падений напряжений на пассивных элементах цепи (резисторах или внут­ренних сопротивлениях источников ЭДС) принимают совпадающими с положительными направлениями токов, протекающих по этим сопро­тивлениям. Положительные направления напряжений U на зажимах иде­альных источников ЭДС противоположны направлениям их ЭДС Е. По­ложительные направления токов и напряжений на участках цепи на схе­мах обозначаются либо стрелкой, либо двойным индексом буквенных обозначений (рис. 3.5).

Если направление обхода контура совпадает с направлением напря­жения, то U записывается в уравнении со знаком «плюс», если не совпада­ет, то со знаком «минус».

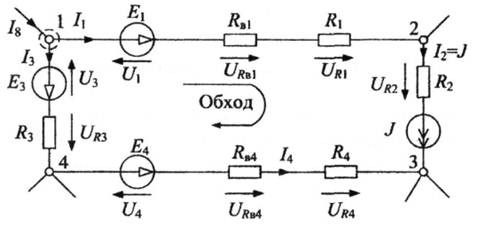
Рис. 3.5. Контур электрической цепи

Согласно второму закону Кирхгофа (3.6), для контура 1-2-3-4-1 (см. рис. 3.5) запишем

-U + U_Rв1 + U_R1+ U_R2 - U_R4 - U_Rв4+ U4- U_R3+ U₃ =0.

При этом перед ЭДС и падениями напряжений ставим знак «плюс», если положительные направления этих величин совпадают с направлением обхода контура, и знак «минус» - в противоположном случае.