Комбинационные схемы. Простейшие комбинационные схемы. Шифраторы, дешифраторы и преобразователи кодов

КОМБИНАЦИОННЫЕ СХЕМЫ

Введение

Комбинационные схемы – схемы, у которых выходное состояние задано только комбинацией входных сигналов.

Рассмотрим пример с тремя переменными (таблица 1).

Таблица 1.

Х1	Х2	Х3	И	ИЛИ		равнозначность	однозначность	2 из 3
0	0	0	0	0	0	1	0	0
0	0	1	0	1	1	0	1	0
0	1	0	0	1	1	0	1	0
0	1	1	0	1	0	1	0	1
1	0	0	0	1	1	0	1	0
1	0	1	0	1	0	1	0	1
1	1	0	0	1	0	1	0	1
1	1	1	1	1	1	0	0	1

Чем больше переменных, тем больше комбинаций.

Простейшие комбинационные схемы.

Пороговое устройство

Есть n равноправных входов.

                              f=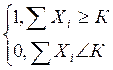

где К это любое число, 1 < К < n

При К=1     f→ или

При К=n     f→ и

Если n – нечетное и К=, то это мажоритарный элемент (схема)

Например – схема 2 из 3.

Как используется этот элемент и для чего нужен?

Пусть есть передатчик и приемник информации (рисунок 1).

    

Рис. 1.

Если произошла помеха (например - молния), то будет ошибка передачи. Мы не защищены от потери информации, вызванной некачественной линией связи.

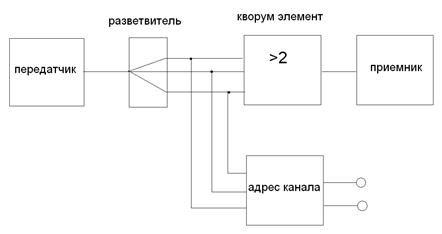
Рис. 2.

Теперь не страшна порча одной из линий связи (рис. 2).

Можно сделать устройство, которое преобразовывает сигналы в номер канала, который испорчен.

Например: если на выходе адрес канала два нуля, то все хорошо. Если две единицы, то третий канал сломан.

Компаратор

Компаратор (рис. 3) – устройство сравнения двух аналоговых сигналов (функция равнозначности).

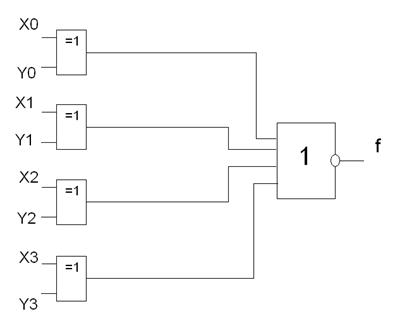
Рис. 3. Компаратор

Если все разряды равны, то на всех выходах будет “0”, после инверсии получится “1”.

Если хотя бы один из разрядов не совпадает, то на выходе “1”, после инверсии - ”0”.

Свертка на четность

Разряд четности: P = X₀ X₁…Xn

 

n+1 – количество разрядов

Х_1…n – разряд числа

Принцип, по которому работает четность (формируется бит четности) показан на рис. 4, 5.

                          

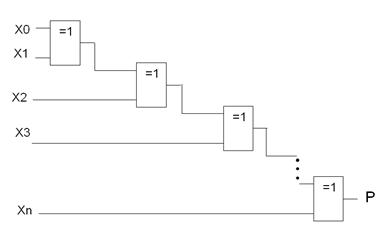
                                                            Рис. 4.

            

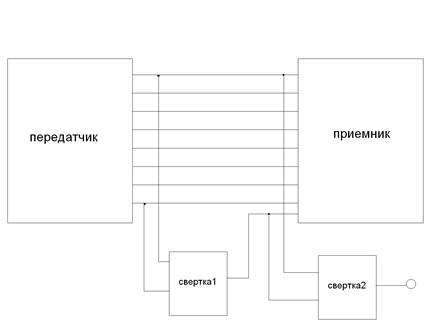
свертка1 – дополняет до четности

  свертка2 – показывает четное число или нет

                                                               Рис. 5.

Недостаток: каждый логический элемент имеет свое время срабатывания, следовательно, существует задержка. Бит четности сформируется спустя сумму времени задержек всех логических элементов.

Пирамидальная схема (рис. 6).

К1554ИП5

                                   

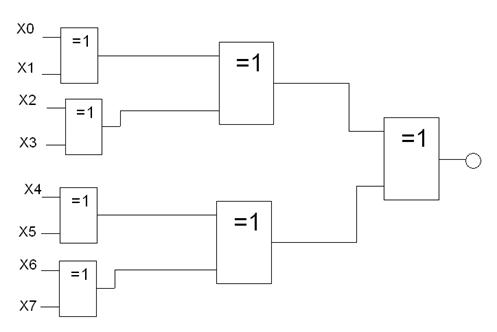
Рис. 6. Пирамидальная схема

Если разрядов больше 8, то используем схему К1554ИП2

Условное обозначение К1554ИП5 и К1554ИП2 на рисунке 7.

                

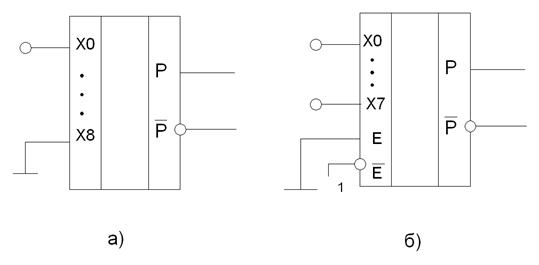
Рис. 7 Условное обозначение:

а) К1554ИП5  б) К1554ИП2

Если хотим использовать схемы для контроля большего числа бит, то рис. 8.

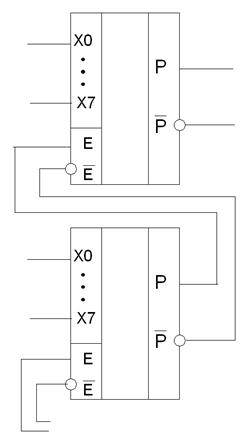
                                                                          Рис. 8.

Шифраторы, дешифраторы и преобразователи кодов

Шифраторы

Шифраторы – схемы для преобразования десятичных чисел в двоичные.

(на схемах обозначается как - CD)

0	1	2	3	4	5	6	7	8	9	8	4	2	1
1	0	0	0	0	0	0	0	0	0	0	0	0	0
0	1	0	0	0	0	0	0	0	0	0	0	0	1
0	0	1	0	0	0	0	0	0	0	0	0	1	0
0	0	0	1	0	0	0	0	0	0	0	0	1	1
0	0	0	0	1	0	0	0	0	0	0	1	0	0
0	0	0	0	0	1	0	0	0	0	0	1	0	1
0	0	0	0	0	0	1	0	0	0	0	1	1	0
0	0	0	0	0	0	0	1	0	0	0	1	1	1
0	0	0	0	0	0	0	0	1	0	1	0	0	0
0	0	0	0	0	0	0	0	0	1	1	0	0	1

Пусть есть 10 кнопок, нужно придумать устройство, которое при нажатии любой кнопки формирует двоично-десятичный код, который будет кодировать число. Рис. 9, 10.

                                           

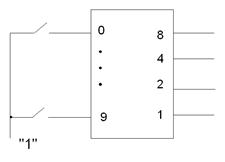
                                                                Рис. 9.       

f₁ = 1 + 3 + 5 + 7 + 9                                                      

(это не цифры, а название переменных!!!)

                                               

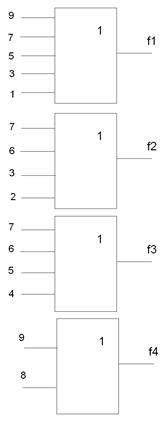
                                                        Рис. 10.

Соответствующие цифры объединяем.

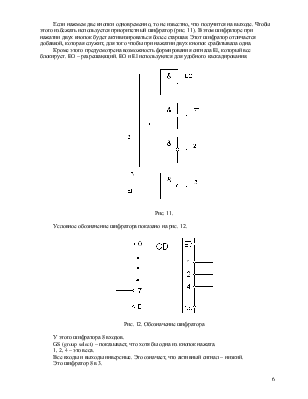
Если нажмем две кнопки одновременно, то не известно, что получится на выходе. Чтобы этого избежать используется приоритетный шифратор (рис. 11). В этом шифраторе при нажатии двух кнопок будет активизироваться более старшая. Этот шифратор отличается добавкой, которая служит, для того чтобы при нажатии двух кнопок срабатывала одна.

Кроме этого предусмотрена возможность формирования сигнала EI, который все блокирует. EO – разрешающий. EO и EI используются для удобного каскадирования.

                                                 

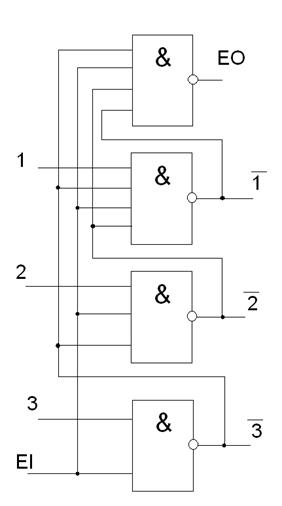
Рис. 11.

Условное обозначение шифратора показано на рис. 12.

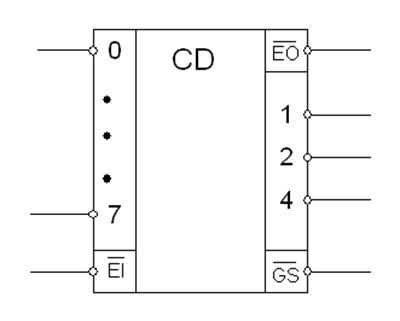
Рис. 12. Обозначение шифратора

У этого шифратора 8 входов.

GS (group select) – показывает, что хотя бы одна из кнопок нажата.

1, 2, 4 – это веса.

Все входы и выходы инверсные. Это означает, что активный сигнал – низкий.

Это шифратор 8 в 3.

Дешифраторы

          Дешифраторы – устройства противоположные шифраторам.

Преобразуют двоичный или двоично-десятичный код в десятичный.

  (на схемах обозначается как - DC).

Шифраторы преобразуют код с большим числом разрядов в код с меньшим, а дешифраторы наоборот.

Примеры дешифраторов:

·  DC 4 в 10 (рис. 13). КР1554ИД10

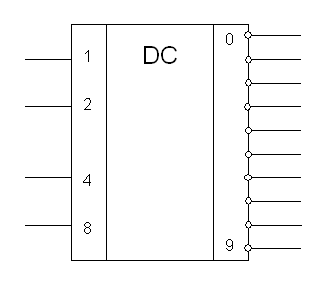
Рис. 13. DC 4 в 10

У этого DC 16 выводов (ножки питания – 2).

·  DC 3 в 8 (рис. 14). КР1554ИД7

                                       

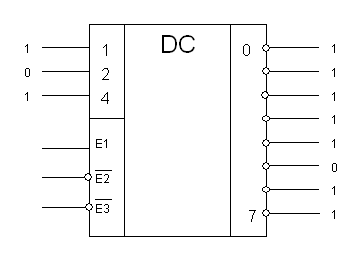
Рис. 14. DC 3 в 8

Входы Е разрешают работу DC. Например, если есть только Е1, то когда он высокий DC работает как надо, а если – низкий, то DC отключается; все выходы пассивны. Если есть только Е3, то когда он низкий, то DC работает и наоборот. Когда присутствует несколько входов Е, то каждый из входов должен быть активным, чтобы DC работал.

            

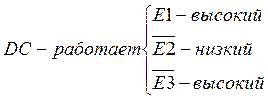
Входы Е нужны чтобы, задавать DC большей разрядности.

·  DC 4 в 16. КР1533ИД1

У этого DC тоже есть входы Е (две штуки).