





6. ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ
Задача
48. Граф ![]() задан матрицей инциденций:
задан матрицей инциденций:
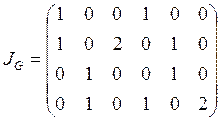 .
.
Требуется:
1) построить граф ![]() ;
;
2) найти степень каждой из его вершин;
3) записать матрицу смежности графа;
4) записать список ребер графа.
Решение.
Граф ![]() является
неориентированным графом, т.к.
является
неориентированным графом, т.к. ![]() не содержит отрицательных
элементов. Число вершин графа равно 4 (по числу строк
не содержит отрицательных
элементов. Число вершин графа равно 4 (по числу строк ![]() ),
число ребер равно 6 (по числу столбцов).
),
число ребер равно 6 (по числу столбцов).
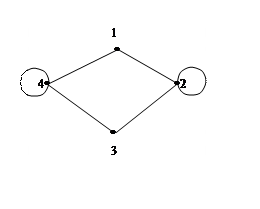 1) Присвоим вершинам графа номера,
сохранив порядок, заданный строками матрицы
1) Присвоим вершинам графа номера,
сохранив порядок, заданный строками матрицы ![]() .
Отметим в произвольном порядке 4 точки, присвоив каждой точке номер.
.
Отметим в произвольном порядке 4 точки, присвоив каждой точке номер.
Просматривая каждый столбец матрицы ![]() , соединяем ребрами вершины
инцидентные данному ребру.
, соединяем ребрами вершины
инцидентные данному ребру.
Если ребро дважды инцидентно вершине
(в матрице ![]() такое ребро помечено "2" в
соответствующей строке), то это ребро является петлей.
такое ребро помечено "2" в
соответствующей строке), то это ребро является петлей.
Выполняя последовательно просмотр всех шести ребер, получаем граф, изображенный на рисунке.
2) Степень вершины графа ![]() – это число ребер, инцидентных
данной вершине. Сложив все числа в строке матрицы
– это число ребер, инцидентных
данной вершине. Сложив все числа в строке матрицы ![]() ,
получим степень соответствующей вершины. Поскольку петли инцидентны вершине
дважды, вклад их в степень вершины равен двум.
,
получим степень соответствующей вершины. Поскольку петли инцидентны вершине
дважды, вклад их в степень вершины равен двум.
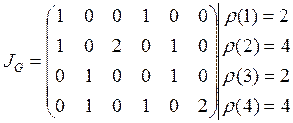 .
.
3) Запишем матрицу смежности графа. В
матрице смежности строки и столбцы соответствуют вершинам графа. Число, стоящее
в ячейке ![]() есть число ребер, соединяющих
вершину
есть число ребер, соединяющих
вершину ![]() с вершиной
с вершиной ![]() ;
;
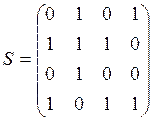 .
.
4) Список ребер графа – это
двустрочная матрица ![]() , в каждом столбце которой
записаны номера вершин, инцидентных данному ребру:
, в каждом столбце которой
записаны номера вершин, инцидентных данному ребру:
![]()
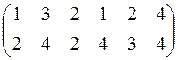 .
.
Задача 49.
Неориентированный граф ![]() задан списком ребер
задан списком ребер 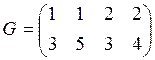 .
.
Требуется:
1) построить граф;
2) записать множество двоичных векторов пространства графа и выделить базис этого пространства;
3) построить все части графа, указав соответствующий вектор пространства графа.
Решение.
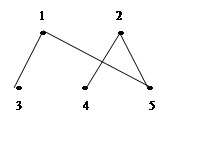 1) Числа в списке ребер – это номера
вершин графа
1) Числа в списке ребер – это номера
вершин графа ![]() . Следовательно данный граф имеет
пять вершин. Построим этот граф.
. Следовательно данный граф имеет
пять вершин. Построим этот граф.
2) Граф ![]() имеет 4 ребра, следовательно пространство
графа
имеет 4 ребра, следовательно пространство
графа ![]() – это множество всех четырехмерных
двоичных векторов. Число таких векторов – 24=16.
– это множество всех четырехмерных
двоичных векторов. Число таких векторов – 24=16.
Запишем эти векторы:
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
Базис данного пространства
векторов составляют векторы ![]() ,
, ![]() ,
, ![]() ,
,
![]() .
.
Любой другой вектор может быть записан как линейная комбинация базисных векторов. Например,
![]()
![]()
![]()
![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() и т.д.
и т.д.
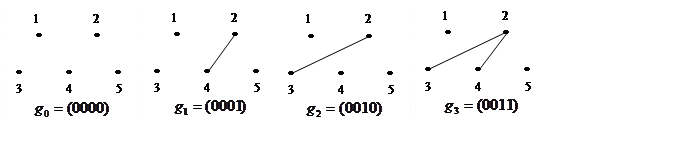 |
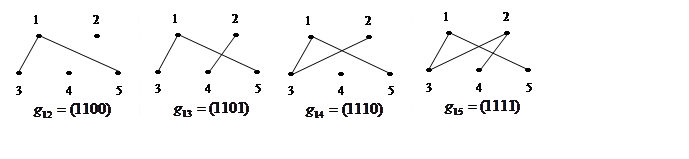
Задача
50. Ориентированный
граф ![]() задан матрицей инциденций:
задан матрицей инциденций:
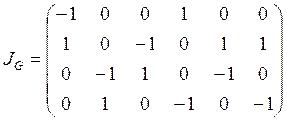 .
.
Требуется:
1) построить граф;
2) построить какой-либо остов и соответствующий ему коостов графа;
3) записать матрицу базисных циклов и матрицу базисных разрезов графа;
4) проверить ортогональность пространства базисных циклов пространству базисных разрезов графа.
 Решение.
Решение.
1) Граф ![]() содержит 4 вершины и 6 ребер. Символ
"1" означает, что ребро выходит из данной вершины, "-1" –
входит в вершину.
содержит 4 вершины и 6 ребер. Символ
"1" означает, что ребро выходит из данной вершины, "-1" –
входит в вершину.
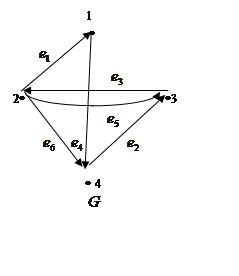
При построении графа введем
обозначения ребер в порядке, задаваемом столбцами матрицы ![]()
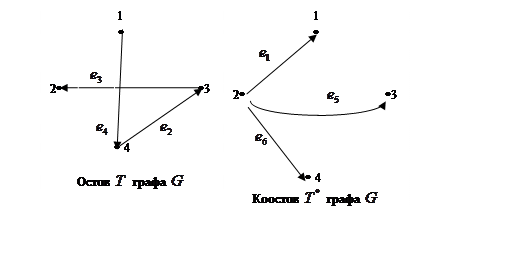 2) Зададим остов графа, обходя его вершины
в направлении ребер. Обход начнем с вершины "1".
2) Зададим остов графа, обходя его вершины
в направлении ребер. Обход начнем с вершины "1".
В коостов графа включаются все ребра графа, не вошедшие в остов.
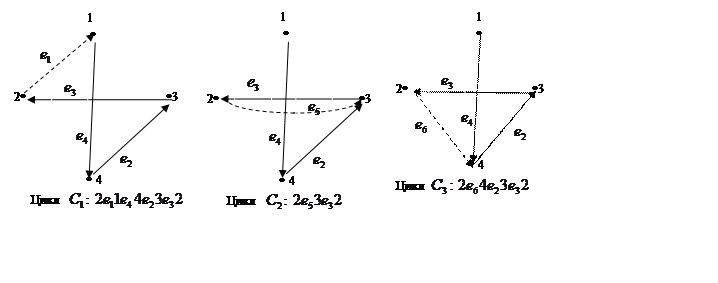 3) Система базисных циклов графа
включает столько циклов, сколько ребер в коостове, в данной задаче – три цикла.
Базисный цикл получают, внося одно из ребер коостова в остов.
3) Система базисных циклов графа
включает столько циклов, сколько ребер в коостове, в данной задаче – три цикла.
Базисный цикл получают, внося одно из ребер коостова в остов.
Запишем базисные циклы матрицей:
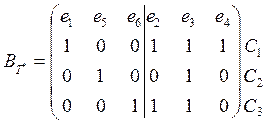
![]() ,
,
где ![]() матрица
базисных циклов, соответствующих коостову
матрица
базисных циклов, соответствующих коостову ![]() ,
, ![]() - ребра коостова,
- ребра коостова, ![]() - ребра остова. Матрица
- ребра остова. Матрица ![]() делится на две части – единичную
матрицу
делится на две части – единичную
матрицу ![]() и матрицу
и матрицу ![]() .
В данном случае все единицы матрицы
.
В данном случае все единицы матрицы ![]() взяты со знаком
"плюс", поскольку при обходе базисных циклов движение происходило в
направлении ребер.
взяты со знаком
"плюс", поскольку при обходе базисных циклов движение происходило в
направлении ребер.
Система базисных разрезов графа включает столько разрезов, сколько ребер в остове, в данной задаче – три разреза. Базисный разрез получают, вынимая одно из ребер остова, остов при этом распадается на две компоненты. Множество ребер, связывающих эти компоненты, и является базисным разрезом.
Первый базисный разрез ![]() получаем, вынув ребро
получаем, вынув ребро ![]() из остова. При этом остов
распадается на компоненты. Первая компонента
из остова. При этом остов
распадается на компоненты. Первая компонента ![]() содержит
вершины 1 и 4, вторая
содержит
вершины 1 и 4, вторая ![]() - вершины 2 и 3. Направление
разреза от
- вершины 2 и 3. Направление
разреза от ![]() к
к ![]() .
.
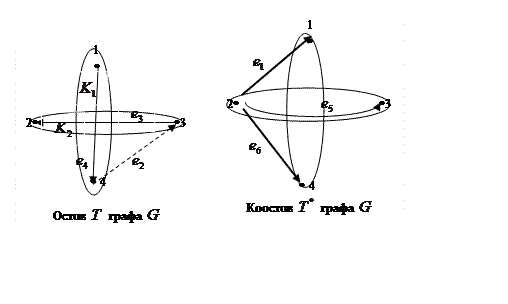 Выделив в коостове полученные
компоненты, видим, что помимо ребра
Выделив в коостове полученные
компоненты, видим, что помимо ребра ![]() они связаны также
ребрами
они связаны также
ребрами ![]() и
и ![]() ,
причем направление этих ребер противоположно направлению разреза.
,
причем направление этих ребер противоположно направлению разреза.
Таким образом первый
базисный разрез ![]() .
.
Аналогично составляем
разрезы ![]() и
и ![]() .
.
![]() ,
,
![]() .
.
Запишем базисные разрезы матрицей:
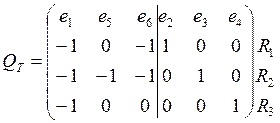
![]() .
.
4) Проверим ортогональность
системы базисных циклов системе базисных разрезов. Для проверки выполним
умножение матрицы ![]() на транспонированную
матрицу
на транспонированную
матрицу ![]() :
:
![]()
![]()
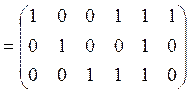
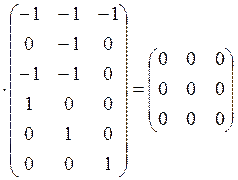 .
.
Так как скалярное произведение любого вектора из системы базисных циклов на любой вектор системы базисных разрезов равно нулю, данные системы векторов ортогональны.
 |
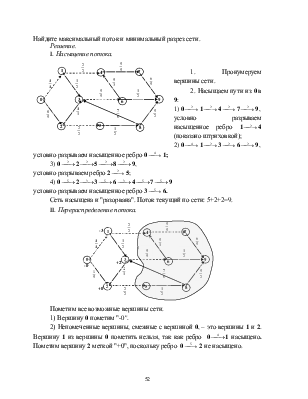
Найдите максимальный поток и минимальный разрез сети.
Решение.
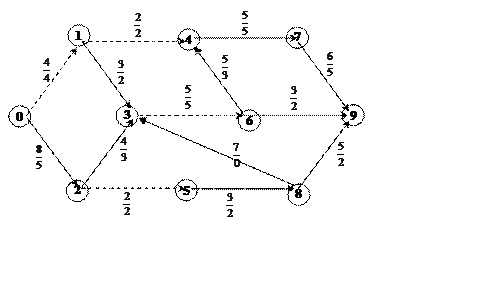 I. Насыщение потока.
I. Насыщение потока.
1. Пронумеруем вершины сети.
2. Насыщаем пути из 0в 9:
1) 0![]() 1
1![]() 4
4![]() 7
7![]() 9,
9,
условно разрываем насыщенное ребро 1![]() 4 (показано штриховкой);
4 (показано штриховкой);
2) 0![]() 1
1![]() 3
3![]() 6
6![]() 9,
9,
условно разрываем насыщенное ребро 0![]() 1;
1;
3) 0![]() 2
2![]() 5
5![]() 8
8![]() 9,
9,
условно разрываем ребро 2![]() 5;
5;
4) 0![]() 2
2![]() 3
3![]() 6
6![]() 4
4![]() 7
7![]() 9
9
условно разрываем насыщенное ребро 3![]() 6.
6.
Сеть насыщена и "разорвана". Поток текущий по сети: 5+2+2=9.

II. Перераспределение потока.
Пометим все возможные вершины сети.
1) Вершину 0 пометим "-0".
2) Непомеченные вершины,
смежные с вершиной 0, – это вершины 1 и 2. Вершину 1 из
вершины 0 пометить нельзя, так как ребро 0![]() 1 насыщено. Пометим
вершину 2 меткой "+0", посколькуребро 0
1 насыщено. Пометим
вершину 2 меткой "+0", посколькуребро 0![]() 2 не насыщено.
2 не насыщено.
3) Непомеченные вершины,
смежные с вершиной 2, – это вершины 3 и 5. Вершину 5 из
вершины 2 пометить нельзя, так как ребро 2![]() 5 насыщено. Пометим
вершину 3 меткой "+2", посколькуребро 2
5 насыщено. Пометим
вершину 3 меткой "+2", посколькуребро 2![]() 3 не насыщено.
3 не насыщено.
4) Непомеченные вершины,
смежные с вершиной 3, – это вершины 1, 6 и 8.
Вершины 5 и 8 из вершины 3 пометить нельзя, так как ребро
3![]() 6 насыщено, а ребро 3
6 насыщено, а ребро 3![]() 8 - пустое. Пометим
вершину 1 меткой "-3", посколькуребро 1
8 - пустое. Пометим
вершину 1 меткой "-3", посколькуребро 1![]() 3 не насыщено.
3 не насыщено.
Никакие другие вершины пометить нельзя. Вершина 9 осталась непомеченной. Следовательно, найденный поток, равный девяти, является максимальным.
Соответствующий
минимальный разрез разбивает множество вершин сети на классы ![]() и
и ![]() .
Все потоки, входящие в
.
Все потоки, входящие в ![]() насыщены, выходящие –
пустые. Мощность разреза равна девяти.
насыщены, выходящие –
пустые. Мощность разреза равна девяти.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.