Арифметические и логические основы цифровой техники

Арифметические и логические основы цифровой техники.

Системы исчисления.

Системы исчисления бывают позиционные и не позиционные.

• Непозиционные – значение цифры не зависит от позиции в числе.

Например: римские цифры.  I I I

• Позиционные – значение цифры зависит от позиции в числе.

1, 11, 111

Основание системы счисления – P, P>1

а₁, а₂,…,а_р – символы алфавита

     А – любое число

А= а_nРⁿ + а_n-1Р^n-1 + …+ а₁Р¹ + а₀Р⁰

Если дробное число, то:

А= а_nРⁿ + а_n-1Р^n-1 + …+ а₁Р¹ + а₀Р⁰ + а_-1Р^-1 + а_-mР^-m   

А=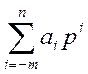

Число выглядит так:  а_nа_n-1…а₁а₀а_-1...а_-m

Рассмотрим пример:  8   2   1,   3   5

                                     а₂  а₁  а₀  а_-1 а_-2

Оптимальная система исчисления.

N – число чисел

n – число разрядов в числе

N=Pⁿ        где   n=log_PN

С – аппаратные затраты – денежное выражение нашей схемы.

С ~ Р·n=Р· log_PN

Минимум функции будет при условии: Р=2,71…, т. е. Р=exp

Т. к. Р – целое, то Р=3 – система оптимальная.(минимальные затраты) Но, она сложна в изготовлении.

Рассмотрим пример. Пусть есть n разрядов, каждый разряд принимает 10 значений, следовательно это десятичная система. При троичной системе каждый разряд будет принимать три значения (0, 1, 2). Но такое устройство более сложное в изготовлении чем, например, при Р=2 (принимает значения - 0,1)

На практике применяют Р=2.

Р=10 в 1,5 раза сложнее, чем Р=2, следовательно затрат больше.

Чем меньше система счисления, тем больше разрядов.

10	2	8	16
0	0	0	0
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F
16	10000	20	10
17	10001	21	11

Двоичная арифметика.

Для суммы:

0+0=0

0+1=1

1+0=1

1+1=10,   где 0 – это сумма S, 1 – это перенос CR

Числа будут записываться как: 00, 01, 01, 10

Таблица истинности:

0	1
1	0

 Для S

0	0
0	1

Для CR     

Для разности:

0-0=0

1-0=1

1-1=0

1·0-1=1    где 1 – это заем

Таблица истинности:

0	1
1	0

Для разности

Для заема

0	1
0	0

Для умножения:

0·0=0

0·1=0

1·0=0

1·1=1

0	0
0	1

Таблица истинности:

Для деления:

0:1=0

1:1=1

Перевод чисел из одной системы в другую.

• 8=2³

           16=2⁴

Примеры: 305,4₈ = 011 000 101, 100_2,    где нижние индексы указывают на систему счисления

     305,4₁₆ = 0011 0000 0101, 01₂

      5F1C, EE₁₆ = 0101 1111 0001 1100, 1110 1110₂

      001010111, 110110100₂ = 127, 664₈

      01010111, 1101 1010₂ = 57, DA₁₆

 

• Система Р и h

А=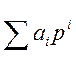

2Е5, А₁₆ = (2·16² + 14·16¹ + 5·16⁰ + 10·16^-1)₁₀ = 741, 625

52₁₀ = 101·1010¹ + 10·1010⁰ = 110100₂

• А = b_n·b_n-1…b₁·b₀ = bn·hⁿ + … + b₁·h¹ + b₀ = (b_n·h^n-1 +… + b₁)·h + b₀ = A₁·h +b₀

Путем деления на основание системы, в которую мы хотим перевести число, будем получать остаток после каждого деления и этот остаток будет составлять цифры числа в новой системе.

Рассмотрим пример:

70₁₀ нужно перевести в двоичную систему

70	2
0	35	2
	1	17	2
		1	8	2
			0	4	2
				0	2	2
					0	1

Следовательно, получаем 1000110

 70₁₀ нужно перевести в «8» систему

70	8
6	8	8
	0	1

Получаем 106

Представление положительных и отрицательных чисел.

Прямой код числа.

Рассмотрим число 0110:

·  Если «+», то 0' 0110

Где 0 показывает что число «+»

·  Если «-», то 1' 0110

Где 1 показывает что число «-»

+0, 0101 запишется как 0,0101

-0, 0101 запишется как 1,0101

Обратный код числа.

	Прямой код	Обратный код	дополнительный
+0110	00110	00110	00110
-0101	10101	11010	11011
+0, 0101	0, 0101	0, 0101	0, 0101
-0, 0101	1, 0101	1, 1010	1, 1011

Обратный код – дополнение до единицы

Дополнительный код – дополнение до двух

Обратный код в сумме с исходным дает 1, а дополнительный в сумме с исходным дает 0.

	Обратный код	Дополнительный код
7	0111	0111
6	0110	0110
5	0101	0101
4	0100	0100
3	0011	0011
2	0010	0010
1	0001	0001
0	0000 1111	0000
-1	1110	1111
-2	1101	1110
-3	1100	1101
-4	1011	1100
-5	1010	1011
-6	1001	1010
-7	1000	1001

Правило сложения для обратного кода: при сложении чисел в обратном коде знаковые разряды складываются аналогично остальным.

Перенос из знакового разряда добавляется к младшему разряду результата.

Правило сложения для дополнительных кодов:при сложении чисел в дополнительном коде знаковые разряды складываются аналогично остальным.

Перенос из знакового разряда теряется, а результат получается в дополнительном коде.

Примеры: в дополнительном коде

·  +4+3=+7

0100+0011=0111

·  1+(-3)=-2