Арифметические и логические основы цифровой техники, страница 2

0001+1101=1110

В обратном коде

·  7+(-3)=4

0111+1100=0100

Весовые коды.

 , где Рⁱ это вес

Вес разряда показывает, на какое число нужно умножить стоящую перед ним цифру алфавита, чтобы получить число в этой системе исчисления.

Для кодировки десятичных чисел в двоичные:

d = W₃·b₃ + W₂·b₂ + W₁·b₁ + W₀·b₀

 

d - десятичная цифра

W – вес данного разряда

b – двоичные цифры

В данном примере 4 двоичных цифры, а это 16 возможных разрядов. Нам надо использовать только 10, следовательно 6 избыточных.

Число вариантов кодировки: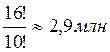

Существуют не весовые коды, которые не подчиняются данной функции.

Самые распространенные весовые коды: 8421, 7421, 7321, 6421, 6321, 5311, 4421, 3331

 8     4   2    1 – двоично-десятичный код

W₃ W₂ W₁ W₀

 

Пример: запишем 6₁₀ в коде 8421

6₁₀ = 8·0 + 4·1 + 2·1 + 1·0 = 0110₈₄₂₁

6₁₀ = 0111₇₃₂₁

6₁₀ = 0110₆₄₂₁

6₁₀ = 0110₃₃₃₁

 Код 8421 совпадает с двоичным, если кодируем числа от 0 до 9.

Весовые коды могут быть отрицательными.

Код 8421 – дополняющий двоично-десятичный код. Его два младших разряда отрицательные (2 и 1)

9₁₀ = 1111₈₄₂₁ = 8·1 + 4·1 – 2·1 - 1·1

Правила составления весовых кодов.

·  Вес любого разряда не должен превосходить больше, чем на единицу сумму весов всех младших разрядов (предыдущих).

·  Вес младшего разряда должен быть единица, иначе мы не сможем закодировать единицу.

·  Вес второго разряда должен быть один или два.

·  Сумма двух старших разрядов должна быть больше либо равна 6, если второй разряд двойка, или 7, если второй разряд единица.

Существуют не весовые коды.

Код 8421 часто используется на практике.

Правила сложения чисел в двоично-десятичном коде (ДДК)

• Если результат получается от 0 до 9, то сложение как двоичных чисел.
• Если результат от 10 до 15, то необходимо произвести коррекцию (добавление 6) и возникающий перенос переносится в старшую тетраду.
• Если результат от 16 до 18, то перенос нужно перенести в старшую тетраду, а потом сделать коррекцию.

Другие виды кодов.

1. Самодополняющиеся коды.

Такой тип кодов, у которых одному числу соответствует другое число, в сумме которые дают единицу во всех разрядах.

Пример: 5₁₀ + 4₁₀ = 9₁₀

               1011₈₄₂₁ + 0100₈₄₂₁ = 1111₈₄₂₁

Коды 2421 и +3 это самодополняющиеся коды.

Код +3 получается из кода 8421 добавлением тройки.  Это непозиционный код. Удобен для вычисления

5₁₀ = 1000₊₃

4₁₀ = 0111₊₃

0₁₀ = 0011₊₃

9₁₀ = 1100₊₃

Свойства сложения чисел в коде +3:

·  Сложение происходит тетрадами, т. е. по четыре разряда

·  Если при сложении есть перенос, то производится коррекция (прибавление 3)

·  Если нет переноса, то производится коррекция с вычитанием тройки.

2. Код Грея.

Это циклический код. Код Грея двух разрядный, у него всегда меняется один разряд. Непозиционный код.

Используется в системах передачи информации.

0	0
0	1
1	1
1	0

0	0	0	0	0
1	0	0	0	1
2	0	0	1	1
3	0	0	1	0
4	0	1	1	0
5	0	1	1	1
6	0	1	0	1
7	0	1	0	0
8	1	1	0	0
9	1	1	0	1

Код Грея:

                                        Четырех разрядный код Грея:    

3. Код 2 из 5

5 разрядов из них лишь два истинные.

4. Код Джонсона

0	0	0	0	0	0
1	0	0	0	0	1
2	0	0	0	1	1
8	1	1	0	0	0
9	1	0	0	0	0

5. Код бикварный.

Это весовой код.

6. Код 51111

Обнаружение и исправление ошибок в кодах.

Кодовое расстояние d – минимальное число бит, которое должно быть изменено при переходе от одного числа к другому.

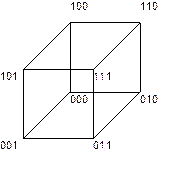
 d=2 между точками 110 и 011

d=1 между соседними точками.

Это кодовое расстояние можно использовать как способ обнаружения ошибки.

Кратность ошибки – (d_min  - 1)

Если изменилось два бита, то двукратной ошибки не обнаружить.

Дополнительные коды увеличивают d, следовательно, помогают избежать ошибки. Например, добавлением бита четности.

Пусть у нас есть число 1011, добавим бит четности, следовательно, получим -  11011 – четное число.

Ошибки при передачи информации возникают всегда.

Пример: у нас есть диск; там 16 битное кодирование, чтобы записать и считать без ошибок добавляется 6 бит, следовательно, получается 22 бита. Это код Рида – Соломона.

На практике используется бит четности по разряду и по времени, чтобы не было двукратных ошибок.

Самое оптимальное кодирование при использовании кода Хэмминга.

Рассмотрим исключающее ИЛИ. 

а	b
0	0	0
0	1	1
1	0	1
1	1	0

            Х = ab                                                           

Бит четности: Р = ABCD

Правила для построения кода Хэмминга:

• Для определенного количества комбинаций двоичных чисел n, определяется число контрольных битов r.

                               

                         m = n - r

n – общее число

m – сама информация

• Контрольные биты занимают позиции I = 1, 2, 4, 8, а биты информации занимают оставшиеся позиции: a₃, a₅, a₆, a₇, a₉, a₁₀
• Вводятся специальные коэффициенты – С

Р – контрольный бит. Он должен быть таким, чтобы сумма единиц с ним была четной.

С₀ = Р₁а₃ а₅ а₇ а₉ а₁₁ а₁₃ а₁₅ = 0

С₁ = Р₂а₃ а₆ а₇ а₁₀ а₁₁ а₁₄ а₁₅ = 0

С₂ = Р₄а₅ а₆ а₇ а₁₂ а₁₃ а₁₄ а₁₅ = 0

С₃ = Р₈а₉ а₁₀ а₁₁ а₁₂ а₁₃ а₁₄ а₁₅ = 0

Если все С = 0, то передача информации прошла без ошибок.

Если хотя бы одно из С не равно 0, то произошла ошибка.

Для обнаружения ошибки существует формула:

N = С_r-1·2^r-1 + … + C_r·2^r + C₁·2 + C₀ ,         где N – номер позиции где произошла ошибка.

Пример:   10101₂,  код 8421

1	0	1	0	1
Х3	Х5	Х6	Х7	Х9

m=5, r=4, n=9

Р₁Р₂Х₃Р₄Х₅Х₆Х₇Р₈Х₉

Р₁=0,  Р₂=0

Р₄=010=1

Р₈=1

001110101_Хэм