Улучшение оценки ковариационной для кластеризации GK

Конспект - это статья представляет два метода, чтобы улучшить вычисление нечеткой матрицы ковариации в GK алгоритм объединения в кластеры. Первый преодолевает проблемы, которые происходят в стандартном GK объединении в кластеры когда число из данных образцы являются маленькими или когда данные в пределах группы линейно коррелированный. Усовершенствование достигнуто, устанавливая отношение между максимальным и минимальным собственным значением ковариации матрица. Второй метод полезен, когда GK алгоритм используется в извлечении нечеткой модели Takagi–Sugeno (TS). Это уменьшает риск переобучения, когда число образцов обучение является низким по сравнению с числом кластеров. Это достигается путем добавления масштабирования матрицы в расчетную матрицу ковариации. Числовые примеры представлены, чтобы демонстрировать преимущество предложенных методов.

I

Введение.

Алгоритм GK [1] является сильным методом  по объединения в кластеры с большим количеством применений в различных областях, включая обработку изображения, классификацию и идентификацию системы [2] [3].

Его главная особенность - локальная адаптация показателя расстояния от формы кластера путем оценки ковариационной матрицы кластера и адаптации расстояния вызывающие матрицы соответственно. Однако численные проблемы часто возникают в стандартной кластеризации GK, когда число выборок данных (в некоторых кластеров) мал или когда данные в кластере (почти) линейно коррелируемы. В таком случае матрица кластер ковариационной становится сингулярной и не может быть инвертирована, чтобы вычислить порождающих норму матрицы. В этой статье представлен способ преодолеть эту проблему сингулярности путем установления соотношения между максимальной и минимальной собственных значений матрицы ковариации. Как видно из примеров, это простая модификация значительно улучшает производительность алгоритма GK. Нечеткой кластеризации также может быть использован алгоритм для извлечения нечетких  правил из данных. Способность алгоритма GK для оценки локальных ковариации и секционирования данных на подмножества, которые могут быть хорошо оснащена линейным суб-моделей, делая его полезным для идентификации моделей TS [4], [3]. Вторая методика, предложенная в данной работе, полезно, когда алгоритм ГК использует извлечение правилами ТС из данных. Это снижает риск переобучения, когда количество обучающей выборки низкий относительно количества кластеров. Это достигается путем добавления масштабирования матрицы единства, с расчетной ковариационной матрицы. Прикладной пример представлен для демонстрации преимущества предлагаемой методики.

II.

Кластеризации GK.

Алгоритм GK [1] основан на итерационной оптимизации целевой функции c-means  типа: [5], [6]:

                                 (1)

Где,  нечеткая матрица разбиения данных  

является прототипом K- класса кластеризации.  является скалярным параметром, определяющим размытости в результате кластеров.

Норма расстояния , может составлять кластеры различной геометрической формы в одном наборе данных:

                                                                            (2)

Метрика каждого кластера определяется местом норм порождающих матриц , которая используется в качестве одного из параметров оптимизации в функции [1]. Это норма позволяет расстоянию адаптироваться к местной топологической структуре данных. Минимизация GK функции объекта достигается за счет использования переменного метода оптимизации в соответствии со следующим известным алгоритмом.

Учитывая набор данных , выбрать количество кластеров , весовой показатель  (обычно 2) , конечное допустимое отклонение  (обычно ) и кластер объемов  (обычно 1). Инициализировать раздел матрицы случайно, так что  (т.е. принадлежит нечеткому разбиение пространства)

Повторите эти действия для

Шаг 1: Средства вычисления кластера:

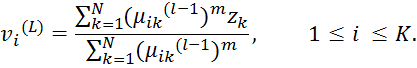
Шаг 2: Вычислить ковариационные матрицы кластера:

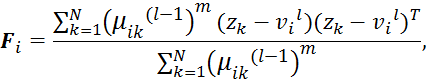
Шаг 3: Вычислить расстояния:

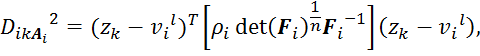
Шаг 4: Обновление раздела матрицы:

для   

если  для  ,

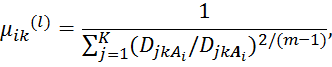
иначе

 для  и

вместе с  иначе.

до тех пор пока .

Вышеуказанные числовые проблемы возникают на шаге 3 алгоритма, где инвертируется ковариационная матрица кластера. Если число выборок данных мал или данные в кластере имеют линейную корреляцию, ковариационная матрица может стать (почти) единственным числом.

III.

Особенности ковариационной матрицы.

Напомним, что собственные значения и векторы ковариационной матрицы, описания формы и ориентации кластеров, см. рис. 1. Если собственное значение равно нулю или соотношение между максимальным и минимальным собственным значением, то условие количество , очень велико (например ) матрица практически единственное число. В таком случае, обратный на шаг 3 не может быть вычислен. Кроме фиксированного объема нормализация не удается определить ( объем ковариационной матрицы) и он становится равным нулю, и следующие формулы таким образом, не могут быть применены: