Улучшение оценки ковариационной для кластеризации GK, страница 2

.                                                          (3)

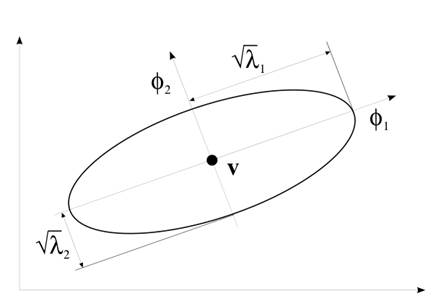
Рис. 1. уравнение  определяет гиперэллипсоид.

Длина оси гиперэллипсоид задается  и его направление, движется на , где  и  это собственное значение и соответствующий собственный вектор , соответственно.

Простой способ избежать численных проблем, ограничить соотношение между максимальным и минимальным собственным значением так, чтобы значение было меньше заданного порога (в нашем примере, мы использовали ). Когда этот порог превышен, минимальное значение увеличивается таким образом, что отношение было равным порогу и ковариационной матрицей восстановления: 

где диагональная матрица, содержащая собственные ограниченные и является матрица, столбцы которой являются соответствующие собственным векторам.

На рисунке  2 показан пример набора данных, которые не могут быть объединены со стандартным алгоритмом GK, из-за численных проблем. Причина в том, что данные образцы в течение трех линейных сегментов полностью коррелируют. Используя описанную выше методику, численные проблемы можно избежать и улучшение алгоритм GK, находясь в предполагаемом разбиение на три линейных сегментов.

Основные направления кластеров идеально совпадают с данными. Эта модель затем объясняет 99,85% дисперсии в данных.

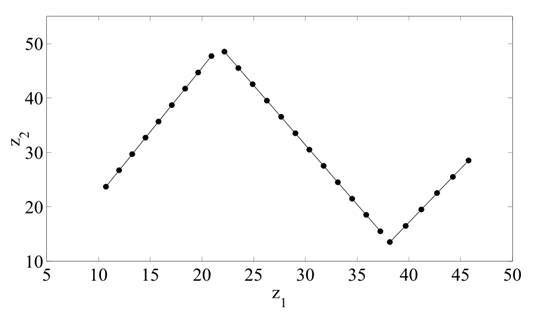
Рис. 2. Пример набора данных с линейными кластерами.

IV.

Проблема переобучения.

Выше модификации алгоритм GK предотвращает работу численных задач. Тем не менее, в результате можно получить кластеры, которые являются чрезвычайно длительны в направлении наибольших собственных значений и имеют мало отношения с реальным распределением данных. Это может привести к переобучения данных и, следовательно, получается плохая модель.

Эта проблема возникает, главным образом, когда количество данных точек в кластере становится слишком небольшой. В таком случае, вычисление ковариационной матрицы не является надежной оценкой исходного распределения данных. Одним из путей решения этой проблемы является ограничение соотношение между максимальными и минимальными собственным значением еще больше, чем описано в предыдущем разделе.

Это позволит предотвратить крайние удлинение кластеров. Другой способ заключается в добавлении масштабной единичной матрицы к ковариационной матрицы. Tadjudin [7] and Friedman [8] описывают несколько различных способов для улучшения оценки ковариации. Вдохновленный этими методами, мы предлагаем следующую оценку для алгоритма ГК:

(4)

где  является параметром настройки и  является ковариационной матрицей всего набора данных. В зависимости от значения  кластеры вынуждены иметь более или менее одинаковую форму.

Где  является 1, все ковариационные матрицы равны и имеют тот же размер, что, конечно, ограничивает возможности алгоритма для правильной идентификации кластеров.

Как  основан на весь набор данных, его значение не зависит от количества кластеров. Объемы , однако, снижаются по мере возрастания количества кластеров. Это означает, что увеличение количества кластеров делает кластеров круглее. Этот термин,  понижает настройка усилия. Формула вес с включенным объем от общего набора данных. Небольшие недостатки этого метода является дополнительным параметром настройки . Однако, при использовании алгоритма GK для извлечения нечетких моделей от автономных данных, как правило, не проблема, чтобы включить дополнительный параметр и настроить его в перекрестной проверке работы. Кроме того, ожидается, что выполнение алгоритма кластеризации уменьшается, когда имеется достаточно данных обучения для построения ковариационной матрицы.

V.

Модификация алгоритма GK.

Полный алгоритм GK, в том числе двух указанных модификаций приведен ниже.

Учитывая набор данных , выбирают стандартные параметры , , , , пороговое условие номера  и весовые параметры . Инициализация раздела матрицы и вычисления ковариационной матрицы всего набора данных.

Повторите эти действия для

Шаг 1: Средства вычисления кластера:

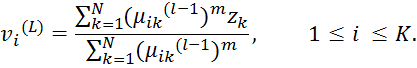
Шаг 2: Вычислить ковариационные матрицы кластера:

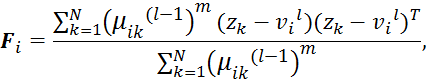
Добавить масштабирование единичной матрицы:

Извлечение собственных  и собственные векторы  для .

Находим  и набор:

    для которых   

Реконструкция  по

Шаг 3: Вычислить расстояния:

 

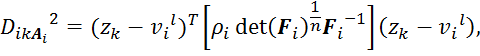
Шаг 4: Обновление раздела матрицы:

для   

если  для  ,

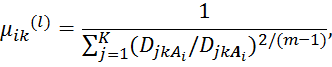
иначе

 для  и

вместе с  иначе.

до тех пор пока .

В двойной точности с плавающей точкой реализации (например, в MATLAB), пороговое условие числа, как правило, быть установлены в большом количестве, например, .

Установка весового параметра  зависит от приложения и некоторые эксперименты могут быть необходимы, чтобы найти правильное значение. MATLAB код алгоритма приведен в Приложении.