Улучшение оценки ковариационной для кластеризации GK, страница 3

VI.

Пример применения.

В этом разделе мы используем алгоритм кластеризации GK построить TS [4] нечетких моделей на основе данных, используя метод, описанный в [3]. Изучаемый процесс является ферментативный Пенициллин-G преобразования. Нечеткая модель описывает, как фермент кинетики зависит от концентрации компонентов в процессе преобразования.

Рассмотрим ферментативное превращение (гидролиз) пенициллин-G (Peng) 6-аминопенициллановой кислоты (АПА) и фенил-уксусной кислоты (PhAH) при рН 8,0 и температуре 310 К под действием фермента пенициллинацилаза. Ожидается, что обменный курс зависит от концентрации PenG, APA and PhAH нелинейным образом и пропорциональна концентрации фермента E:

PenG, APA, PhAH)

где нелинейная функция , неизвестно. Данные из 10 партий эксперимента начались при различных начальных условиях, были использованы для создания TS нечеткой модели для . Данные были получены от лабораторных экспериментов, выполненных в перемешивании термостатируют лаборатории биореакторе объемом 1500 см3. Настройки лаборатория приведена на рис. 3. Подробнее об этом процессе можно найти в [9].

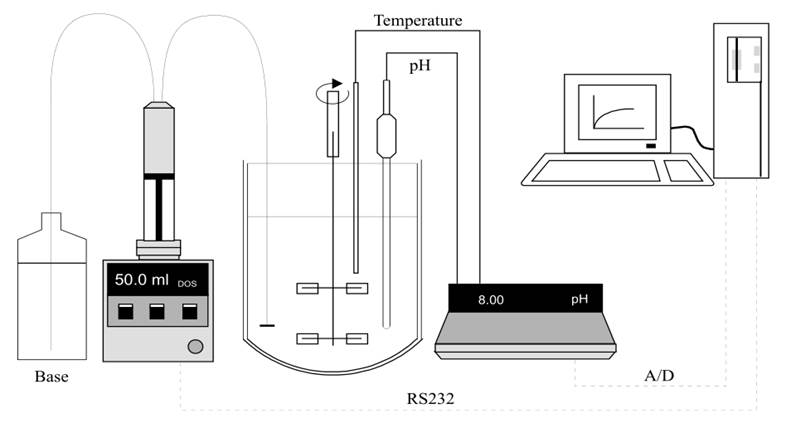
Рис. 3. Экспериментальная установка.

В общей сложности 816 точек данных было доступно для идентификации. Дополнительные эксперименты проводились с целью проверки модели. Некоторые типичные экспериментов показаны на рис. 4. TS Правила имеют следующий вид:

Функции принадлежности , и, как следствие параметры , находятся через кластеризацию GK в декартовой пространства  . Обратите внимание, что идентификация эксперимента не была достаточно захватывающей систему и данные могут быть тесно связаны в четырехмерном пространстве кластеризации . Это подтверждается, наблюдая за результатами стандартного алгоритма ГК, который не может найти кластеры для K> 2 (см. таблицу, где "-" означает, что кластеризация не удалось из-за численных проблем). При ограничении максимального отношение собственные численные проблемы можно избежать. Более чем 3 кластера, однако, производительность полученной модели уменьшается. При единичной матрице добавляется в соответствии с уравнением (4),

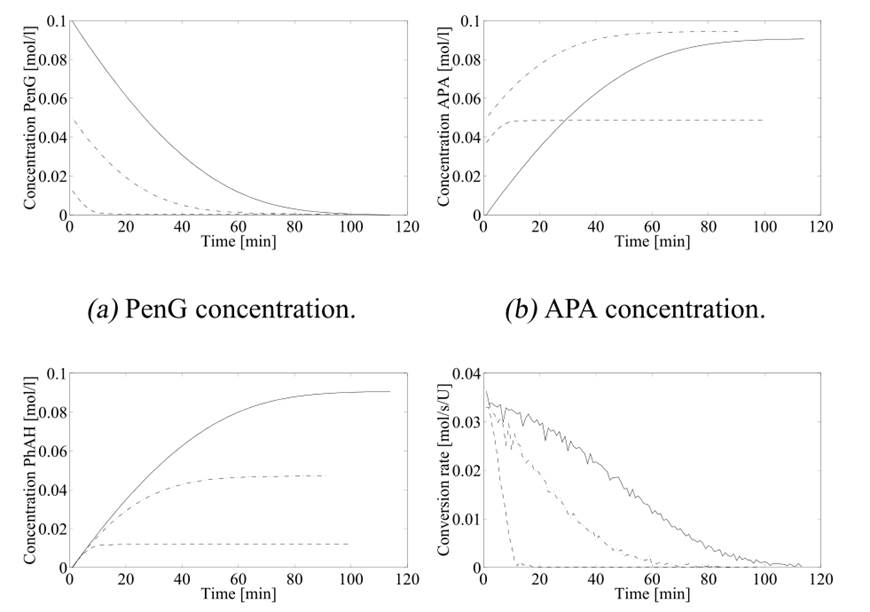
(c) PhAH концентрации.                                               (d) Обменный курс повторно.

Рис. 4. Экспериментальные данные из некоторых типичных экспериментов партии. Три кривые каждого графика отражают эксперименты начала с разных исходных условий.

эффективность модели остается примерно на том же уровне. То же самое верно, когда собственные ограничения.

Таблица 1.

ВЫПОЛНЕНИЕ НЕЧЕТКОЙ МОДЕЛИ С РАЗЛИЧНЫМИ МЕТОДАМИ ОЦЕНКИ КОВАРИАЦИИ.

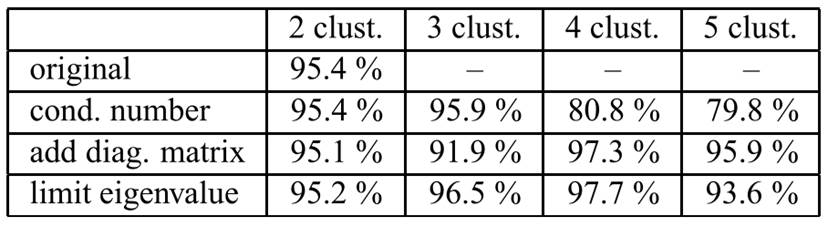
Все параметры оставались одинаковы для разных методов (даже случайная инициализация алгоритма). Выходные данные модели рассчитывается с использованием 4-кратной проверкой. Производительность полученной модели по сравнению с помощью дисперсии составляли (VAF) индекса, определяется по формуле:

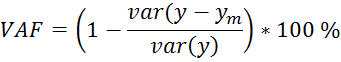
где  измеренный выход системы и  выходной модели.VAF 100% означает идеальный модель прогнозирования.

VII.

Выводы.

В этой статье мы предложили метод, чтобы избежать численных задач, которые могут возникнуть при вычислении норму порождающих матрицы в алгоритм кластеризации Густафсон-Кессель (GK).

Это решение не изменит производительность алгоритма, но гарантий, что она всегда в состоянии найти разбиение данных. При использовании алгоритма кластеризации GK построить Тагаки-Сугено нечеткие модели, определенная степень переобучения будут испытываться для большего числа кластеров. В таком случае производительность может быть улучшена путем дальнейшего ограничения максимального соотношения между собственным значениям ковариационной матрицы или путем добавления масштабированного единичной матрицы для матрицы ковариации. Хотя такие изменения могут улучшить производительность для небольших наборов данных, с достаточным количеством обучающих выборок, это ограничение в свободе алгоритма может оказать негативное влияние и на производительность. Некоторые эксперименты с весовой параметр , таким образом, могут быть необходимы. GK нечеткой кластеризации и идентификации программного обеспечения для MATLAB можно загрузить с http://Lcewww.et.tudelft.nl/˜babuska.

Подтверждение.

Авторы благодарят Kluyver Лаборатория биотехнологии Технологический университет Делфта за предоставление данных.

ПРИЛОЖЕНИЕ: Густафсон-Кессель Алгоритм

В этом приложении мы приведем реализацию MATLAB модифицированного алгоритма GK.

Отправить по электронной почте R.Babuska@its.tudelft.nl чтобы получить копию М-файл.

Ссылки.