Министерство образования Российской Федерации
Государственное образовательное учреждение высшего
профессионального образования
«Комсомольский-на-Амуре Государственный Технический Университет»
Лабораторная работа 1
по курсу «Теория вычислительных процессов»
Выполнил студент группы 1ВТ-2: Журавлёв Д.А.
Преподаватель: Абарникова Е.Б.
2004
Тема: Стратегии поиска решений в графе пространства состояний.
Цель: Научится производить поиск решений на графе пространства состояний.
Задание: разработать программу обхода шахматной доски конем. Конь должен побывать в каждой клетке один раз. Метод поиска решения: поиск решения в фиксированном множестве пространств – образовать и проверить.
Стратегия поиска решения: в глубину.
Теоретический материал:
Граф – множество вершин вместе с множеством ребер. Каждое ребро задается парой вершин. Если ребра направлены, то называются дугами. Дуги задаются упорядоченными парами. Такие графы называются направленными. Ребрам можно приписывать имена или метки, в зависимости от конкретного приложения.
Графы можно представлять:
Каждое ребро – отдельное предложение:
link ( a, b ).
link ( b, c ).
Весь граф – как один объект, состоящий из двух множеств: множество вершин и множество ребер ( дуг ). Каждое множество - список
G = graf ( [ a, b, c, d, e ], [ p( a, b ), p( b, c ),…,p( d, e ) ] ).
Для направленного графа:
G1= graf ( [ a | _ ], [ d( a, b, 1 ), d( b, c, 4 ) …] )
Типичные операции:
а) Найти путь между двумя заданными вершинами.
б) Найти подграф, обладающий некоторыми заданными свойствами.
Более подробно остановимся на задаче поиска пути в графе.
Пусть G – Гамильтонов граф. А, Е – вершины
path ( A, E, G, P ). // путь Р в G от А к Е.
path ( a, e, G, [ a, b, c, e ] ).
path ( a, e, G, [ a, b, c, d, e ] ).
Один из методов поиска пути:
Если А=Е, то Р=[ А ], иначе найти Р1 из произвольной К в Е, а затем – путь из А в К не пересекающий вершин Р1. Так как путь не должен проходить через вершины Р1, определяем
path1 ( A, P1, G, P ). // А – некоторая вершина, G – граф, Р1 – путь в G,
path ( A, Е, G, P ): - path1 ( A, [ E ], G, P ). // идущий из А в начальную вершину Р1, а затем – вдоль Р1.
Существует граничный случай, когда А=К ( начальная вершина Р1). Если они не совпадают, то А - > L - > K - > E
К – смежная с L
L не принадлежит Р1
Для Р выписывается отношение path1 ( A, [ L | P1], G, P ).
Если граф G представлен как пара множеств, назовем отношение как смежный ( near ).
G = graf (V, D ), где V= [ a, b, c, d, e ], D= [ d( a, b, 1 ), d( b, c, 4) … ].
Отношения принадлежности элемента списку:
sod ( duga ( X, Y ), D ).
near ( L, K, graf ( V, D )): - sod ( duga ( L, K ), D ).
Поискпути
path ( A, E, G, P ): - path1 ( A, [ E ], G, P ).
path1 ( A, [ A | P1 ], _ , [ A | P1 ] ).
path1 ( A, [ K | P1 ], G, P1 ): - near ( L, K, G),
sod ( L, P1 ),
path1( A, [ L, K | P1], G, P ).
Пространство состояний – граф, вершины которого соответствуют ситуациям, встречаются в задаче, а решение сводится к поиску пути в этом графе. Дуги – разрешенные переходы из одного состояния в другое.
Конкретная задача определяется:
а) Пространством состояний б) Стартовой вершиной в) Целевым условием – условием, к достижению которого надо стремиться. Целевые волны – волны, удовлетворяющие этим условиям.
Принцип работы программы:
Граф пространства состояний (для стартовой клетки (1;1)):
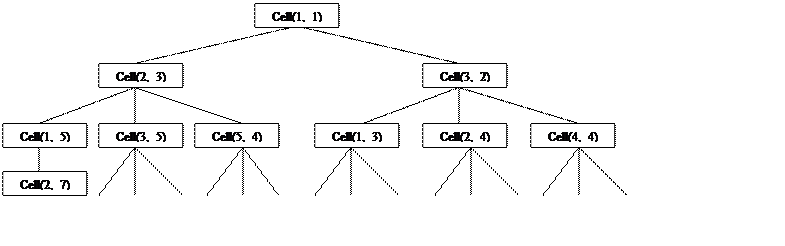 |
Сравнение стратегий поиска.
|
Стратегия поиска |
Скорость |
Память |
|
В глубину |
Медленный |
Мало памяти |
|
В ширину |
Быстрый |
Много памяти |
Описание программы:
Пользователь с помощью мыши задает начальную клетку обхода. На этой клетке появляется значок в виде коня. Затем пользователь может запустить программу на выполнение кнопку “Обход”. При этом программа просчитывает ходы коня и отображает на поле результат - порядковые номера позиций обхода.
Если пользователь не ввел стартовую клетку, программа начинает обход из верхнего левого угла доски.
В разделе “Информация” создается список ходов и отлеживается процесс обхода. При старте в поле отображается начальная клетка.
При нажатии кнопки "Выход" производится выход из программы.
Через меню программы можно вызвать данные об авторах (пункт ”О программе”) и справку (пункт ”Справка”).
Данным методом невозможно реализовать полный обход доски из-за слишком высоких требований к объёму необходимой памяти. Поэтому, по завершении обхода, на доске остаются не пройденные клетки, обозначенные цифрой -1.
Основные предикаты:
Помимо встроенных в Prolog типов данных, в программе были определены следующие типы пользователя:
1) i = integer – целое число.
2) cell = cell(i,i,i) – клетка доски.
3) desk = cell* - список всех клеток доски.
В программе использовались следующие ,базы данных:
1) path (desk)
2) start (cell)
Помимо встроенных в Prolog системных предикат, в программе были определены следующие предикаты пользователя:
|
Предикат |
Описание |
|
fillDesk(i,i,desk,desk) |
инициализация списка всех клеток доски |
|
updatePicture(desk) |
восстановление пути при обновлении экрана |
|
drawLine(i, i, i) |
прорисовка номеров ходов |
|
del(cell, desk, desk) |
удаление элемента из списка |
|
add(cell, desk, desk) |
добавление элемента в список |
|
mem(cell, desk) |
проверка на принадлежность элемента списку |
|
findPath(cell, desk) |
общий предикат обхода шахматной доски |
|
cellSelect(cell,desk,cell) |
вспомогательный предикат обхода доски |
|
mouseCheck (i,i) |
обработка выбора клетки с помощью мыши |
Файл MAIN.INC:
DOMAINS
i = integer
cell = cell(i,i,i)
desk = cell*
CONSTANTS
picX = 10
picY = 10
mFree = -1
cellWH = 32
picSize = 273
DATABASE - db
path (desk)
start (cell)
flag(i)
PREDICATES
fillDesk(i,i,desk,desk)
del(cell, desk, desk)
add(cell, desk, desk)
mem(cell, desk)
findPath(cell, desk)
cellSelect(cell,desk,i)
updatePicture(desk)
drawLine(i, i, i)
mouseCheck (i,i)
filllbox(i,desk)
CLAUSES
% инициализация списка всех клеток доски
fillDesk(8,8,X,[cell(8,8,mFree)|X]):-!.
fillDesk(I,8,X,Y):-I1=I+1,!,fillDesk(I1,1,[cell(I,8,mFree)|X],Y).
fillDesk(I,J,X,Y):-J1=J+1,!,fillDesk(I,J1,[cell(I,J,mFree)|X],Y).
% удаление элемента из списка
del(X,[X|L],L):-!.
del(X,[Y|L],[Y|L1]):-del(X,L,L1).
% добавление элемента в список
add(X, Y, [X|Y]).
% проверка на принадлежность элемента списку
mem (X, [X|_]):-!.
mem (X, [_|T]):- mem(X, T).
drawLine (I, J, N):X = (J-1)*cellWH+cellWH/3+picX+6, Y = I*cellWH-cellWH/3 + picY+6,
X1 = (J-1)*cellWH+picX+13, Y1 = (I-1)*cellWH + picY+13,
X2 = X1+cellWH-10, Y2 = Y1+cellWH-15,
W = vpi_GetTaskWin (), win_SetForeColor(W, color_White),
Pen = pen(3,ps_Solid,color_Blue), Brush = brush(pat_Solid, color_Blue),
win_setpen(W, Pen), win_setBrush(W,Brush),
R = rct(X1, Y1, X2, Y2), draw_Ellipse(W, R),
str_int(S, N), draw_Text(W, X, Y, S).
% восстановление пути при обновлении экрана
updatePicture([]).
updatePicture( [cell(I, J, M)|T] ):drawLine (I, J, M),
updatePicture(T).
cellSelect(cell(I, J, M), Dsk, C):M=55,
assert(path(Dsk)),
!.
cellSelect(cell(I, J, M), Dsk, C):I1=I-2, J1=J-1,
mem(cell(I1,J1,mFree), Dsk),
del(cell(I1,J1,_), Dsk, Dsk2), M3 = M+1,
add(cell(I1,J1,M3), Dsk2, Dsk3),
C1=C+1,
cellSelect(cell(I1, J1, M3), Dsk3, C1)
,!.
cellSelect(cell(I, J, M), Dsk, C):I1=I-2, J1=J+1,
mem(cell(I1,J1,mFree), Dsk),
del(cell(I1,J1,_), Dsk, Dsk2), M3 = M+1,
add(cell(I1,J1,M3), Dsk2, Dsk3),
C1=C+1,
cellSelect(cell(I1, J1, M3), Dsk3, C1)
,!.
cellSelect(cell(I, J, M), Dsk, C):I1=I-1, J1=J+2,
mem(cell(I1,J1,mFree), Dsk),
del(cell(I1,J1,_), Dsk, Dsk2), M3 = M+1,
add(cell(I1,J1,M3), Dsk2, Dsk3),
C1=C+1,
cellSelect(cell(I1, J1, M3), Dsk3, C1)
,!.
cellSelect(cell(I, J, M), Dsk, C):I1=I+1, J1=J+2,
mem(cell(I1,J1,mFree), Dsk),
del(cell(I1,J1,_), Dsk, Dsk2), M3 = M+1,
add(cell(I1,J1,M3), Dsk2, Dsk3),
C1=C+1,
cellSelect(cell(I1, J1, M3), Dsk3, C1)
,!.
cellSelect(cell(I, J, M), Dsk, C):I1=I+2, J1=J+1,
mem(cell(I1,J1,mFree), Dsk),
del(cell(I1,J1,_), Dsk, Dsk2), M3 = M+1,
add(cell(I1,J1,M3), Dsk2, Dsk3),
C1=C+1,
cellSelect(cell(I1, J1, M3), Dsk3, C1)
,!.
cellSelect(cell(I, J, M), Dsk, C):I1=I+2, J1=J-1,
mem(cell(I1,J1,mFree), Dsk),
del(cell(I1,J1,_), Dsk, Dsk2), M3 = M+1,
add(cell(I1,J1,M3), Dsk2, Dsk3),
C1=C+1,
cellSelect(cell(I1, J1, M3), Dsk3, C1)
,!.
cellSelect(cell(I, J, M), Dsk, C):I1=I+1, J1=J-2,
mem(cell(I1,J1,mFree), Dsk),
del(cell(I1,J1,_), Dsk, Dsk2), M3 = M+1,
add(cell(I1,J1,M3), Dsk2, Dsk3),
C1=C+1,
cellSelect(cell(I1, J1, M3), Dsk3, C1)
,!.
cellSelect(cell(I, J, M), Dsk, C):I1=I-1, J1=J-2,
mem(cell(I1,J1,mFree), Dsk),
del(cell(I1,J1,_), Dsk, Dsk2), M3 = M+1,
add(cell(I1,J1,M3), Dsk2, Dsk3),
C1=C+1,
cellSelect(cell(I1, J1, M3), Dsk3, C1)
,!.
% обход шахматной доски
findPath(cell(I,J,M), Dsk):-
cellSelect( cell(I,J,M), Dsk,0),
path(D),
filllbox(1,D),
updatePicture(D),
!.
mouseCheck(X, Y):J=X div cellWH, I = Y div cellWH, I<8, I>=0, J<8, J>=0,
X2 = J*cellWH+picX+6, Y2 = I*cellWH+picY+6, I1=I+1, J1=J+1,
retractall(path(_)), retractall(start(_)), assert(start(cell(I1,J1,1))),
W = vpi_GetTaskWin(),
H4 = win_getctlhandle(W, idc_edit),
H5 = win_getctlhandle(W, lst_list), lbox_clear(H5),
N1 = 'a'+J1-1, format (Str, "Начальная клетка: %c%d", N1, I1),
win_SetText(H4, Str),
win_Invalidate(W), sleep(20), draw_Icon(W, X2, Y2, idi_kon).
filllbox(M, Dsk):-
M=55,
!.
filllbox(M, Dsk):-
del(cell(I,J,M), Dsk, Dsk2), M2 = M+1,
W = vpi_GetTaskWin(), H = win_getctlhandle(W, lst_list),
N1 = 'a'+J-1, format (Str, "%-2d. %c%d", M, N1, I),
lbox_Add(H, Str),
filllbox(M2, Dsk2),!.
Программа и методика испытаний
Испытуемая программа RGZ.exe предназначена для обхода доски шахматным конём, так чтобы он побывал в каждой клетке один
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.