Аучится производить операции с нечеткими числами

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«Комсомольский – на - Амуре государственный технический университет»

Кафедра математического обеспечения и применения ЭВМ

ЛАБОРАТОРНАЯ РАБОТА № 4

По курсу: «Теория вычислительных процессов и структур»

Студенты группы 4ВС-1:                                                                               Киселевский М.Е.

Алексеенко Н.С.

Преподаватель:                                                                                              Жбанов С.А.

2007 г.

Тема:                         Нечеткие числа.

Цель работы:          Научится производить операции с нечеткими числами.

Задание:                    Написать программу, производящую сложение 2-х нечетких чисел.

Теоретическое описание

Размытое число – используется для обозначения нечетко определяемой величины, таких как “около 5”.

Размытое число – это любое подмножество , где x – число на прямой действительных чисел R, .

Два размытых числа равны тогда и только тогда, когда их функции членства равны. Размытое число может быть представлено в дискретной и непрерывной форме.

а) Представление в дискретной форме.

Дискретное размытое число – это матрица специального вида, верхняя и нижняя строки, которые связаны между собой.

U	30	40	50	60	70	80	90
mA(ui)	0,3	0,5	0,8	1,0	0,7	0,5	0,3

б) Непрерывная функция – число представляется функцией  

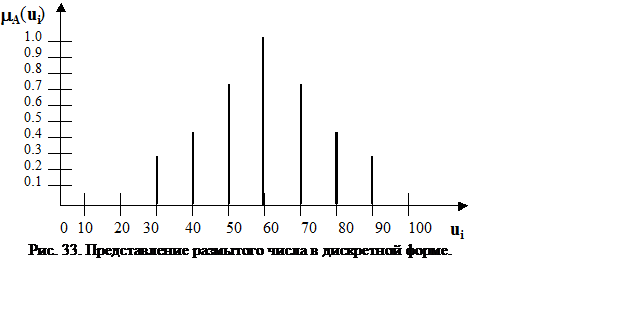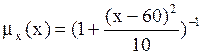
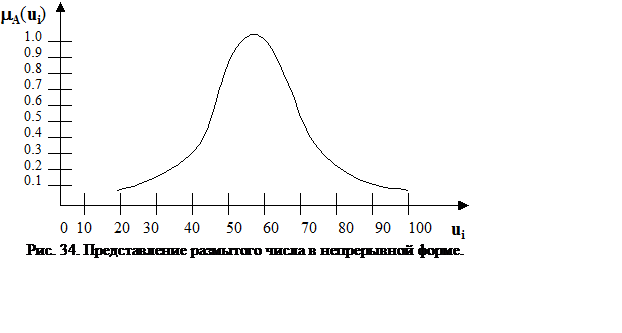Сложение двух размытых чисел:           

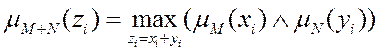                                                   (6.31)

Пример: Пусть даны следующие размытые числа: M – “целые, близкие к 3”, N – “целое, близкое к 2”.

xi, yi	0	1	2	3	4	5	6
mM(xi)	0	0,3	0,8	1,0	0,5	0,1	0
mN(yi)	0	0,6	1,0	0,9	0,4	0	-

Рассмотрим пример получения m_M+N(z_i) при  z = 6

Чтобы получить z = 6,  возможны варианты сочетаний x и y:

x	0	1	2	3	4	5	6
y	6	5	4	3	2	1	0
mM(xi)	0	0,3	0,8	1,0	0,5	0,1	0
mN(yi)	-	0	0,4	0,9	1,0	0,6	0
mM(xi) Ù mN(yi)	0	0	0,4	0,9	0,5	0,1	0

Аналогично вычисляются значения m_M+N(z_i) для других значений z_i = x_i+y_i:

zi = xi+yi	1	2	3	4	5	6	7	8	9	10
mM+N(zi)	0	0,3	0,6	0,8	1	0,9	0,5	0,4	0,1	0

Результат вычислений можно интерпретировать как «целое число, близкое к 5»

Сложность операций над размытыми числами и их ранжирования привела к тому, что стараются использовать нечеткие множества.

Описание предикатов

nondeterm preaddx(WINDOW) – добавление в базу данных значения нечёткого числа X.

nondeterm preaddy(WINDOW) – добавление в базу данных значения нечёткого числа Y.

nondeterm drawx(WINDOW) – прорисовка заголовка информации о нечётком числе X.

nondeterm drawy(WINDOW) – прорисовка заголовка информации о нечётком числе Y.

nondeterm drawz(WINDOW) – прорисовка заголовка информации о нечётком числе Z.

nondeterm drawallx(WINDOW,ILIST,integer) – прорисовка заголовка информации о нечётком числе X.

nondeterm drawally(WINDOW,ILIST,integer) – прорисовка заголовка информации о нечётком числе Y.

nondeterm drawallz(WINDOW,ILIST,integer) – прорисовка заголовка информации о нечётком числе Z.

nondeterm drawelem(WINDOW,integer,integer,integer,real) – прорисовка некоторого нечёткого числа.

nondeterm bubble_sort(ILIST,ILIST) – пузырьковая сортировка.

nondeterm permit(ILIST,ILIST) – перестановка элементов в списке.

myasserttoz(integer,real,real) - добавление в базу данных значения нечёткого числа Z.

nondeterm analize(string) – запуск анализа данных.

getmax(ILIST,real,real) – получение максимальной степени уверенности в списке.

nondeterm countmax(ILIST,real,integer,integer) – подсчёт количества максимальных степеней уверенности.

nondeterm getanswer(ILIST,real,integer,string) – получение ответа.

countelems(ILIST,integer,integer) – подсчёт количества элементов в списке.

checkforconstancy(ILIST,real) – проверка на корректность данных.

getlastelem(ILIST,integer) – получение последнего элемента списка