Решение задач с помощью алгоритма перебора с возвратом

Министерство образования и науки РФ

ГОУВПО «Комсомольский-на-Амуре государственный технический университет»

Кафедра математического обеспечения и применения ЭВМ

Лабораторная работа №2

По дисциплине «СиАОД»

Вариант №4

Исполнитель:

Зимин А.В.

Студент гр. 4ВС-1

Руководитель:

Хусаинов А.А.

Комсомольск-на-Амуре

2007

Постановка задачи

Решить задачу с помощью алгоритма перебора с возвратом.

Задание по варианту: Решить задачу коммивояжера методом перебора с возвратом. Цены билетов заданы с помощью симметричной  n´n  матрицы.

Алгоритм

Задача коммивояжера заключается в следующем: имеется  nгородов и известны цены билетов. Коммивояжер должен посетить все nгородов по одному разу, вернувшись в тот, с которого начал. Требуется найти такой маршрут движения, при котором суммарная цена билетов будет минимальной. Схема маршрутов задана графом (см. рис. 1). Данная задача сводится к поиску гамильтонова цикла в графе с минимальной суммой стоимостей путей между узлами.

Для решения задачи необходимо перебрать все гамильтоновы циклы и найти среди них цикл наименьшей стоимости.

Путь будем представлять в виде последовательности вершин (x₁,x₂,…,x_k). Такой путь будет простым если и только если x_i ¹  x_j для всех i¹j, i,jÎ{1,2,…,k}.

Определим предикаты.

P_k(x₁,x₂,…x_k)=1 Û x_i¹x_j, при 1 £ i < j £ k, и {x_i,x_i+1} – ребра при 1 £ i < k;

Q(x₁,x₂,…x_k)=1 Û k=n и {x_n,x₁} – ребро.

Для того, чтобы последовательности вершин (x₁,x₂,…x_k) удовлетворяли условию x_i¹x_j, будем раскрашивать вершины этих последовательностей и учитывать раскраску при выборе очередей вершины. Гамильтонов цикл, с началом x₁=n₀, представим как последовательность (x₁,x₂,…,x_n,x_n+1), где x_n+1=x₁=n₀.

Пусть A_k – множество вершин, смежных с x_k, c_n - раскраска вершины n_.  Согласно общей схеме алгоритма перебора с возвратом, получаем следующий алгоритм для перебора гамильтоновых циклов:

void Gamilton(int k)

{

for(yÎA_k)

{

if((k==n+1)&&(y==v)) вывод x₁,…,x_k,x₁)

else if(c[y]==0)

{

x_k=y; c[y]=1;

Gamilton(k+1);

c[y]=0;

}

}

}

void main()

{

for(vÎV) c[v]=0; // V – множество всех вершин графа

x₁=v₀; c[v₀]=1; Gamilton(2);

}

 

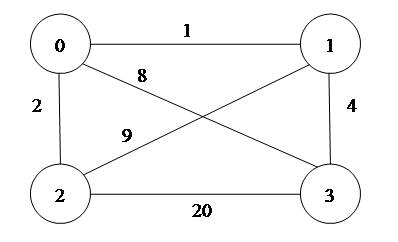Рис. 1. Граф, задающий схему маршрутов

Текст программы

//--------------------------------------------------------------------------#include <vcl.h>

#pragma hdrstop

#define n 4

#include "Unit1.h"

//--------------------------------------------------------------------------#pragma package(smart_init)

#pragma resource "*.dfm"

TForm1 *Form1;

//--------------------------------------------------------------------------__fastcall TForm1::TForm1(TComponent* Owner)

: TForm(Owner)

{

}

//--------------------------------------------------------------------------int c[n] ;       // номер хода, на котором посещается вершина

int path[n];     // номера посещаемых вершин

int rez_path[n];// путь с наим. стоимостью

int v0=0;       // начальная вершина

int sum[n];

int min=3200;   //мин. стоимость

int a[n][n] =

{

0,1,2,8,

1,0,9,4,

2,9,0,20,

8,4,20,0

};

void prnt(void)

{

int i, temp=0;

for ( i = 0 ; i<n ; i++)

{

temp+=sum[i];

}

temp+=a[path[n-1]][0];

if(temp<min)

{ 

min=temp;

for (i=0; i<n; i++)

{

rez_path[i]=path[i];

}

}

}

//подпрограмма нахождения гамильтонова цикла

int gamilton (int k)

{

int v,q1=0;

for(v=0; v<n; v++)

{

if(a[v][path[k-1]]||a[path[k-1]][v])

{

if (k==n &&  v==v0 ) prnt();

else if (c[v]==-1)

{

c[v] = k;

path[k]=v;

sum[k]=a[v][path[k-1]];

gamilton (k+1);

c[v]=-1;

} else continue;

}

}      return q1;

}

void mainfunc()

{

int i;

String text = "";

for(i=0;i<n;i++) c[i]=-1;

path[0]=v0 ;

c[v0]=v0;

if(gamilton (1)) prnt();

for(i=0; i<n; i++)

{

text = text + IntToStr(rez_path[i]) + " ";

Form1->Edit1->Text = text;

}

text = text + "0";

Form1->Edit1->Text = text;

Form1->Edit2->Text = IntToStr(min);

}

void __fastcall TForm1::Button1Click(TObject *Sender)

{

mainfunc();

}

//---------------------------------------------------------------------------

Результат работы программы