Нахождение остовного леса минимального веса с помощью метода Крускала

Министерство образования и науки РФ

ГОУВПО «Комсомольский-на-Амуре государственный технический университет»

Кафедра математического обеспечения и применения ЭВМ

Лабораторная работа №4

По дисциплине «СиАОД»

Вариант №4

Исполнитель:

Зимин А.В.

Студент гр. 4ВС-1

Руководитель:

Хусаинов А.А.

Комсомольск-на-Амуре

2007

Постановка задачи

Найти остовной лес минимального веса с помощью метода Крускала.

Вершины графа – точки плоскости. Веса ребер равны расстояниям между точками.

Алгоритм

Пусть задан простой связный граф (V, E) с функцией w: E ® R, w(e) ³ 0  для всех e Î E. Требуется построить покрывающее дерево T минимального веса . Будем разбивать множество вершин на попарно непересекающиеся подмножества. (Разбиение осуществляется с помощью раскраски вершин в разные цвета. Вершины одинакового цвета образуют подмножество, являющееся элементом разбиения.) Сначала рассматриваем разбиение R = {{v}: v Î V}, состоящее из всех одноэлементных подмножеств. Полагаем множество ребер T пустым. Затем перебираем рёбра e Î E, у которых концы имеют разные цвета. Из них выбираем ребро наименьшего веса и присоединяем его к T. Все вершины графа, цвета которых совпадают с цветами концов выбранного ребра, перекрашиваем в один цвет. Процесс повторяется до тех пор, пока все вершины графа не будут окрашены в один цвет.

В результате получим остовной лес минимального веса. Если заданный граф несвязен, то получим остовное дерево минимального веса.

Опишем алгоритм Крускала более подробно:

Шаг 0.  Задан граф (V, E). Множество ребер E задано в виде последовательности рёбер e₁, e₂, …, e_n в порядке неубывания весов w(e₁) £ … £ w(e_n).

Шаг 1.  T = Æ; R = {{v}: v Î V}.

Шаг 2.  (Цикл для i = 1, 2, …, n) Если e_i = {u, v} , где u Î A, v Î B; A, B Î R,         A ¹ B, то установить  и .

Текст программы

//--------------------------------------------------------------------------#include <vcl.h>

#pragma hdrstop

#include "Unit1.h"

//--------------------------------------------------------------------------#pragma package(smart_init)

#pragma resource "*.dfm"

//--------------------------------------------------------------------------#define n 5

#include <process.h>

#include <math.h>

TForm1 *Form1;

//--------------------------------------------------------------------------__fastcall TForm1::TForm1(TComponent* Owner)

: TForm(Owner)

{

Form1->Image1->Canvas->Refresh();

}

//--------------------------------------------------------------------------int kor[n][2]= {{100,190}, //0

{150,50},  //1

{450,100},  //2

{300, 300},  //3

{320, 205}}; //4

//0, 1, 2, 3, 4

float matrix[n][n]={{0, 1, 0, 1, 1},//0

{1, 0, 1, 0, 1},  //1

{0, 1, 0, 1, 1},  //2

{1, 0, 1, 0, 1},  //3

{1 ,1 ,1 ,1 ,0}};//4

int color[n]; //раскраска вершин графа

void h(int **x, int k)

{

int i;

for (i = 0; i<k; i++)

{

Form1->Image1->Canvas->MoveTo(kor[x[i][0]][0], kor[x[i][0]][1]);

Form1->Image1->Canvas->LineTo(kor[x[i][1]][0], kor[x[i][1]][1]);

}

}

//находим вес ребер

void rast()

{

float d;

for(int i=0;i<n;i++)

{

for(int j=0;j<n;j++)

{

if(matrix[i][j]>0) //если есть путь из вершины i в вершину j

{

//Веса ребер равны расстояниям  между точками.

matrix[i][j]=sqrt(pow(kor[j][0]-kor[i][0],2)+pow(kor[j][1]-kor[i][1],2));

}

}

}

}

void mainf()

{

int i,j;

int ii=0;

int **ver;

int **mst;

ver = (int**)calloc(8, sizeof(int*));

mst = (int**)calloc(8, sizeof(int*));

for(i=0;i<8;i++)

{

ver[i] =  (int*)calloc(2, sizeof(int));

mst[i] =  (int*)calloc(2, sizeof(int));

}

float L=0;

rast();              //заполнить массив весов ребер

//закрашиваем все i вершины графа разным цветом

for(i=0;i<n;i++) color[i]=i;

//найдем все ребра и запишем в массив

for(i=0;i<n-1;i++)//перебираем все точки

for(j=i+1;j<n;j++) //смотрим все номера вершин после i

{

if(matrix[i][j]>0) //если есть пусть из т. i в т. j

{

ver[ii][0]=i;//точка - начало ребра

ver[ii][1]=j;//точка - конец ребра

ii++;

}

}

h(ver, 8);

//сортируем ребра по неубыванию весов

for(i=0;i<n*2-2;i++)

{

for(j=i+1;j<n*2-2;j++)

{

if(matrix[ver[i][0]][ver[i][1]]>matrix[ver[j][0]][ver[j][1]])

{

int tmpi,tmpj;

tmpi=ver[i][0];

tmpj=ver[i][1];

ver[i][0]=ver[j][0];

ver[i][1]=ver[j][1];

ver[j][0]=tmpi;

ver[j][1]=tmpj;

}

}

}

ii=0;

int col;

col=color[ver[0][0]];

//находим миним остновное дерево

for(i=0;i<n*2-2;i++)

{

if (col!=color[ver[i][1]]&&col==color[ver[i][0]]||col!=color[ver[i][0]]&&col==color[ver[i][1]])

{

if (col!=color[ver[i][0]]) color[ver[i][0]]=col;

if (col!=color[ver[i][1]]) color[ver[i][1]]=col;

mst[ii][0]=ver[i][0];

mst[ii][1]=ver[i][1];

ii++;

}

}

Form1->Image1->Canvas->Pen->Color=clRed;

h(mst, ii);

Form1->Image1->Canvas->Pen->Color=clBlack;

//общая сумма

for(i=0;i<ii;i++) L+=matrix[mst[i][0]][mst[i][1]];

Form1->Edit1->Text =  L;

}

void __fastcall TForm1::Button1Click(TObject *Sender)

{

mainf();

}

//---------------------------------------------------------------------------

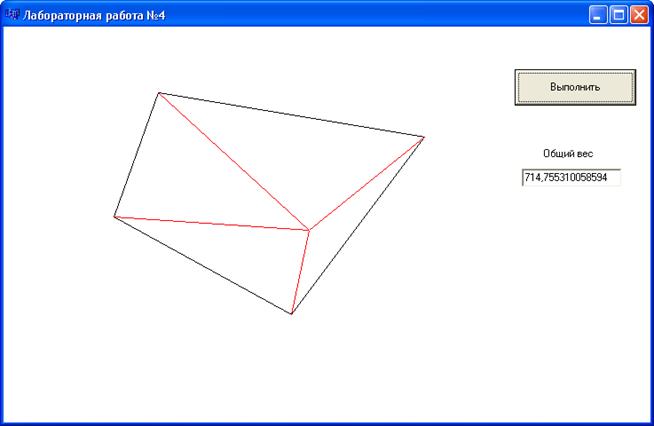
Результат работы программы