ЛАБОРАТОРНАЯ РАБОТА 1
Написать программу перебора слов, функций или чисел, удовлетворяющих заданным условиям. Каждое слово, функция или последовательность чисел выводится с новой строки. Числа m и n вводятся с клавиатуры.
1. Перебрать все функции f:{0,1,…,m-1} ® {0,1,…,n-1}.
2. Перебрать все сюръекции f:{0,1,…,m-1} ® {0,1,…,n-1}.
3. Перебрать все инъекции f:{0,1,…,m-1} ® {0,1,…,n-1}.
4. Перебрать все монотонно неубывающие функции f: [m] ® [n].
5. Перебрать все монотонно возрастающие функции f :[m] ® [n].
6. Перебрать все монотонно неубывающие сюръекции f: [m] ® [n].
7. Перебрать все монотонно невозрастающие функции f: [m] ® [n].
8. Перебрать все монотонно неубывающие функции f: [m] ® [n].
9. Перебрать все монотонно невозрастающие сюръекции f: [m] ® [n].
10. Перебрать все слова длиной не более n, составленные из букв "а" и "b".
11. Найти слово длины n, составленное из букв "a", "b", "c" и "d", не содержащие смежных идентичных (равных) подтекстов.
12. Найти слово длины n, составленное из букв "a", "b", и "c", не содержащие смежных инверсно равных подтекстов.
13. Перебрать все слова длины n, составленные из букв "a", "b" и "c", не содержащие смежных инверсно равных подтекстов.
14. Вывести на экран все десятичные числа, состоящие не более чем из n ненулевых цифр, у которых стоящие рядом цифры отличаются не более чем на 1.
15. Вывести на экран все последовательности натуральных чисел (x1, x2,…,x2n), таких, что 0 £ xi £ m, и x1 £ x2 ³ x3 £ … ³ x2k-1 £ x2k ³ x2k+1 £ … ³ x2n-1 £ x2n.
16. Вывести на экран все последовательности натуральных чисел (x1, x2,…,xn), таких, что 0 £ xi £ m, и x1 < x2 > x3 < … > x2k-1 < x2k > x2k+1 < … > x2n-1 > x2n.
17. Организовать перебор последовательностей x[1], x[2],…,x[n], удовлетворяющих условиям 1 £ x[k] £ k и x[x[k]] = x[k] для всех k=1,2,3,…,n. Вывести результаты при n=4 и при n=5.
18. Организовать перебор последовательностей x1 >…> xm таких, что n ³ x1 и xm³0.
19. Организовать перебор последовательностей целых чисел n ³ x1 ³ … ³ xm ³ 0.
20. Организовать перебор последовательностей целых чисел 0 £ x1 £ … £ xm £ n.
21. Перебрать последовательности неотрицательных целых чисел x1,x2,…,xm, сумма квадратов которых x12 + x22 + … + xm2 равна n.
22. Вывести на экран десятичные числа, состоящие из последовательностей n монотонно неубывающих цифр.
23. Вывести на экран все десятичные числа, состоящие из строго возрастающих последовательностей не равных между собой цифр.
24. Вывести на экран все десятичные числа, состоящие из строго убывающих последовательностей не равных между собой цифр.
25. Вывести на экран десятичные числа, состоящие из последовательностей не более чем n невозрастающих цифр.
26. Найти
сумму 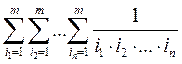 .
.
27. Найти
произведение 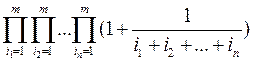 .
.
28. Найти
сумму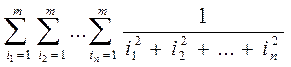 .
.
29. Найти
сумму дробей 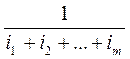 по всем подмножествам {i1, i2,
… , im} множества {1,
2, …, n}.
по всем подмножествам {i1, i2,
… , im} множества {1,
2, …, n}.
30. Найти
произведение 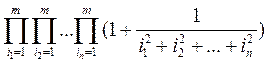 .
.
Пояснения к заданию 1. Функцией f:{a1,…am}®{b1,…bn} называется такое множество пар, для которого выполнены следующие условия:
· Для каждого xÎ{a1,…am} существует такой yÎ{b1,…bn}, что (x,y)Îf; иными словами, область определения отношения f равна всему множеству {a1,a2…am};
· Если (x,y1)Îf и (x,y2)Îf, то y1=y2; для произвольной функции f:{a1,…,am}®{b1,…bn} и элемента xÎ{a1,…am} существует единственный элемент yÎ{b1,…bn}, для которого (x,y) Îf. Обозначим этот элемент через f(x).
Функция f:{a1,…am}®{b1,…bn} называется сюръективной (сюръекцией), если для каждого yÎ{b1,…bn} существует xÎ{a1,…am}, такой, что y=f(x). Очевидно, что при m<n таких функций не существует. Функция f:{a1,…am}®{b1,…bn} называется инъективной (или инъекцией), если верна импликация x1¹x2 Þ f(x1) ¹f(x2).
Обозначим через [k] множество {0,1,…,k}. Функция f:{0,1,…,m}®{0,1,…,n} называется монотонно неубывающей, если f(0) £f(1) £…£f(m),
- монотонно невозрастающей, если f(0) ³f(1) ³…³f(m),
- убывающей, если f(0) >f(1) >…>f(m),
- возрастающей, если f(0) <f(1)<…<f(m).
Словом называется произвольная последовательность букв. Длиной слова x1x2…xn, составленного из букв xi, называется число n. Пустое слово имеет длину 0. Подсловом, или подтекстом слова x1x2…xn, называется слово, равное для некоторых i и j, 1 £ i £ j £ n, слову xixi+1…xj. Подтексты xixi+1…xj и xj+1xj+2…xk называются смежными. Два слова x1x2…xm и y1y2…yn называются идентичными или равными, если m=n и для всех 1 £ i £ m и имеют место равенства xi=yi. Два слова x1x2…xm и y1y2…yn называются инверсно равными, если m=n и справедливы равенства y1=yn, x2=yn-1,…,xi=yn-i+1,…,xn=y1.
Отметим, что в варианте 23 максимально возможное количество цифр в числах равно 9, а в варианте 24 максимально возможное количество – 10.
Задание.
Найти сумму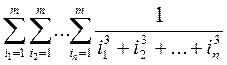 .
.
Решение. Напишем подпрограмму double sum3(int m, int n), зависящую от m и n, основанную на методе построения m вложенных циклов, и используем
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.