Решение задачи с помощью алгоритма перебора с возвратом

Министерство образования Российской Федерации

Государственное образовательное учреждение высшего

профессионального образования

«Комсомольский-на-Амуре Государственный Технический Университет»

Факультет компьютерных технологий

Кафедра МОП ЭВМ

ЛАБОРАТОРНАЯ РАБОТА 2

СиАОД

Студентка группы 1 ВТ 1:                                      Кондырева Т.В.

Преподаватель:                                                            Изабеков З.А.

Комсомольск-на-Амуре

2004 г.

 Задание:

Решить задачу с помощью алгоритма перебора с возвратом.

Вариант 8:

1.  Задано множество A = {a₁,a₂,…a_n}, натуральные числа s(a_i)>0, и k>0. Найти разбиение 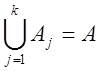 множества А на попарно непересекающиеся подмножества,  при котором 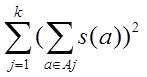минимальна.

Решение:

Разбиением множества A={a₁,a₂,…,a_n} называется множество его подмножеств B₁,B₂,…,B_k таких, что B_iÇB_j=Æ для всех 1£i<j£k, и 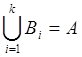. Для перебора разбиений можно предполагать, что A={1,2,3,…,n}.

Наш метод будет основан на построении разбиений множества {1, 2,…, n}, исходя из разбиения множества {1, 2,…, n-1}. Если построено разбиение {B₁, B₂,…, B_k} множества {1, 2,…, n-1}, то легко найти следующие разбиения множества {1, 2,…, n}:

B₁È{n}, B₂,…, B_k,

B₁, B₂ È{n},…, B_k,

…

B₁, B₂,…, B_k È{n}_,

B₁, B₂,…, B_k,{n}.

такой подход позволяет генерировать все разбиения множества {1, 2,…, n}, исходя из всех разбиений множества {1, 2,…, n-1}.

Каждое разбиение множества {1,2,…, n} будем представлять как последовательность блоков, упорядоченных по возрастанию самого маленького элемента в блоке. Этот наименьший элемент блока мы будем называть номером блока. Для каждого элемента i, 1 £ i £ n, номер блока, содержащего элемент i, будем хранить в элементе block[i].

Разработаем рекурсивную подпрограмму, аргументом которой служит k>0, генерирующую из разбиения множества {1, 2,…, k-1} продолжающие его разбиения множества {1,2,…,k}. Опишем подпрограмму подробнее. Пусть получено разбиение множества {1, 2,…, k-1}, определенное с помощью массива block[1], …, block[k-1]. Тогда j пробегает элементы 1, 2, …, k-1, и, как только j попадет в некоторый блок, став равным наименьшему элементу этого блока block[j] = j, к этому блоку добавим элемент k  с помощью операции block[k] = j. Получаем новое разбиение, которое в случае k = n выводиться на экран. В случае k<n вызывается функция rec(k+1). Кроме значений j = 1, 2,…, k-1 рассматривается j = k, в этом случае новый блок разбиения будет состоять из единственного элемента k. Приходим к следующему тексту программы:

Текст программы:

#include<stdio.h>

#include<conio.h>

#define n 4

int block[n+1];

int s[4]={1,2,3,4};

int temp;

void rec(int k)

{

int i,j,m,sum,sum1,priz=0;

for (i=0;i<n;i++) temp=s[i]+temp;

temp=temp*temp;

for(j=1;j<=k;j++)

{

if(block[j]==j) block[k]=j;

else if (j==k) block[k]=k; else continue;

if(k==n)

{

printf("\n");

sum=0;  sum1=0;

for (i=1;i<=n;i++)

{

for(m=1;m<=n;m++)

{if (block[m]==i)

sum1=s[m-1]+sum1;

}

sum1=sum1*sum1;

sum=sum+sum1;

sum1=0;

}

if (sum<=temp)

{     clrscr();

printf("%d\n",sum);

temp=sum;

for (i=1;i<=n;i++)

{   priz=0;

for(m=1;m<=n;m++)

if (block[m]==i)

{if (priz==0) {printf("(");priz++;}

printf(" %d ",m);}

if (priz==1) printf(")");

}

}

}

if (k<n) rec(k+1);

}

}

void main()

{clrscr();

int i;

for (i=0; i<=n; i++) block[i]=0;

block[1]=1;

rec(2);

getch();

}

В результате мы получаем разбиения множества {1, 2, 3, 4}:

( 1 2 3 4 )

( 1 2 3 )( 4 )

( 1 2 4 )( 3 )

( 1 2 )( 3 4 )

( 1 2 )( 3 )( 4 )

( 1 3 4 )( 2 )

( 1 3 )( 2 4 )

( 1 3 )( 2 )( 4 )

( 1 4 )( 2 3 )

( 1 )( 2 3 4 )

( 1 )( 2 3 )( 4 )

( 1 4 )( 2 )( 3 )

( 1 )( 2 4 )( 3 )

( 1 )( 2 )( 3 4 )

( 1 )( 2 )( 3 )( 4 )

Но из всех выберется только то разбиение, для которого 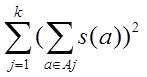минимальна.

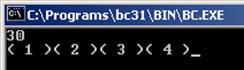
Результат работы программы: