Метод художника для удаления невидимых частей поверхностей

Задача № 1. Метод художника для удаления невидимых частей поверхностей.

Метод художника - это простой метод изображения поверхностей с удалением невидимых линий. Пусть поверхность определяется непрерывной функцией z=f(x,y), а переменные x и y изменяются в прямоугольнике на плоскости Oxy: x_min £ x£ x_max, y_min£ y£ y_max. Рассматривается прямоугольная сетка в плоскости Oxy с шагом hx=(x_max-x_min)/nx по x, и hy=(y_max-y_min)/ny по y. Каждому прямоугольнику ((x_i,y_j), (x_i,y_j+1), (x_i+1,y_j+1), (x_i+1,y_j)), 0£ j£ nx-1, 0£ i£ ny-1 на плоскости Oxy соответствует четырехугольник (f(x_i,y_j), f(x_i,y_j+1), f(x_i+1,y_j+1), f(x_i+1,y_j)) в пространстве Oxyz. Будем приближать поверхность z=f(x,y) многогранником, состоящим из таких закрашенных четырехугольников. На экран будем выводить проекции закрашенных четырехугольников.

В методе художника выводятся все закрашенные четырехугольники, а удаление невидимых частей поверхности происходит автоматически за счет порядка вывода закрашенных четырехугольников. Последовательно выводятся все закрашенные четырехугольники, но от дальних к ближним. При этом ранее выведенные на экран невидимые части четырехугольников «закрываются» четырехугольниками, выведенными позже. Элементом изображения в этом методе является закрашенный четырехугольник.

Пример. Если требуется методом художника вывести изображение человека на фоне дерева, то сначала строится закрашенное изображение дерева, включая ту часть дерева, которая позже будет закрыта изображением человека, а затем строится закрашенное изображение человека.

Задача № 2. Задан отрезок с экранными координатами ((1, 1), (6, 3)). Рассмотреть на примере  этого отрезка алгоритм Брезенхема и записать последовательность точек, которые будут сгенерированы этим алгоритмом.

x0=1, y0=1, x1=6, y1=3

dx=x1-x0=6-1=5, dy=y1-y0=3-1=2 -0.5<=d<0.5, dx>0, dy>0, dx>dy

1.  (1,1) d=0

2.  x++, d+=dy/dx; x=2, d=0.4; (2,1)

3.  x++, d+=0.4=0.8, y++, d=d-1=-0.2, x=3, y=2; (3,2)

4.  x=4, d=-0.2+0.4=0.2, y=2; (4,2)

5.  x=5, d=0.2+0.4=0.6, y=3, d=0.6-1=-0.4 (5,3)

6.  x=6, d=-0.4+0.4=0, y=3 (6,3)

Задача № 3. Пусть известны координаты точки S(2, 4, 5) и плоскость P, которая задаётся векторами u₁ = (0, 1, 0), u₂ = (0, 0, 1) и r₀ = (1, 1, 1). Найти координаты (x′, y′) параллельной проекции точки S на плоскость P в направлении вектора u = (1, 0.4, 0.5).

r=S, r-r0=(1,3,4)

(U1,U2,U)=1

x’=(r-r0,U2,U)=2.6

y’=(r-r0,U1,U)=-3.5

Задача № 4. Разработать программу, которая выводит на экран график функции y =1/(x-2) для -4≤ x ≤4 и -4≤ y ≤4.

#include <graphics.h>

#include <math.h>

#include <conio.h>

#include <stdio.h>

float xmin, xmax;                  // Область изменения x

float ymin, ymax;                  // Область изменения y

float hx;                          // Шаг

float xdens, ydens;

// Вычислениеэкранной x координаты

int ex(float x,float y)

{return (int) ((x-xmin)/xdens);}

// Вычислениеэкранной y координаты

int ey(float x,float y)

{return (int) ((ymax-y)/ydens);}

// Функция y=f(x)

float f(float x) {return (float)1/(x-2);}

main()

{

int graphdriver= DETECT, graphmode, n=100;

float x,y;

// Инициализация графического режима:

initgraph(&graphdriver,&graphmode,"C:\\BC\\BGI");

// параметры:

Xmin=-4,xmax=4;

Ymin=-4,ymax=4;

xdens=(xmax-xmin)/getmaxx(); //Вычисление коэффициента масштабирования по x

ydens=(ymax-ymin)/getmaxy(); //Вычисление коэффициента масштабирования по y

hx=(xmax-xmin)/n;                            // Вычисление шага

setcolor(7);                          // Установка цвета для вывода осей

setcolor(15);                         // Установка цвета для графика функции

// Вывод графика функции 1/x-2

for(x=xmin;x<xmax;x+=hx)

line(ex(x,f(x)),ey(x,f(x)), ex(x+hx, f(x+hx)), ey(x+hx, f(x+hx)));

getch();               // Ожидание нажатия любой клавиши

closegraph (); // Выход из графического режима

}

Задача № 5. Пусть известны координаты точки S(2, 5, 3) и плоскость P, которая задаётся векторами u₁ = (0, 1, 0), u₂ = (0, 0, 1) и r₀ = (0.3, 0.7, 0.2). Найти координаты (x′, y′) центральной проекции точки S на плоскость P из точки наблюдения r_v = (1, 1, 1).

r=S, rv-r0=(0.7,0.3,0.8), r-rv=(1,4,2)

(U1,U2,r-rv)=1

(rv-r0,U2,r-rv)=-2.5

x’=-2.5/1=-2.5

(rv-r0,U1,r-rv)=0.6

y’=-0.6/1=-0.6

Задача № 6. Пусть заданы координаты точки (1, 2, 3), единичный вектор 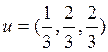 и угол φ=180⁰. Найти координаты (x′, y′, z′) точки после поворота ее на угол φ вокруг вектора u.

r'=A*r

A=UU^T+cos φ(E- UU^T)+sin φ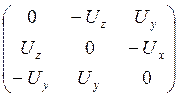

UU^T=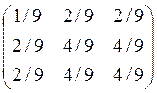

E- UU^T=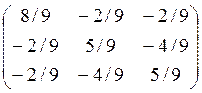

cos φ(E- UU^T)=-1* E- UU^T=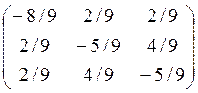

sin φ=0

A=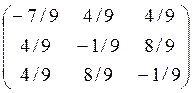

(x′, y′, z′)=*=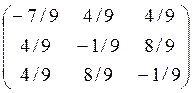

Задача № 7. Разработать программу, которая выводит на экран график функции x =2t-t², y =3t-t³ для -4≤ x ≤4 и -4≤ y ≤4.